Chào ace, bài này chúng ta sẽ tìm hiểu về Binary Search Tree trong series tự học về cấu trúc dữ liệu(CTDL) và giải thuật, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, độ phức tạp, ứng dụng của nó, code ví dụ…) về nó thông qua các phần sau.
Sau đây là định nghĩa về Binary Search Tree (BST) – Cây nhị phân tìm kiếm theo Wikipedia:
Binary Search Tree, là một cấu trúc dữ liệu cây nhị phân dựa trên cơ sở các nodes, Binary Search Tree có các tính chất sau:
– Phần cây con bên trái của một node nào đó chỉ chứa các nodes có key (giá trị/data) nhỏ hơn key của node đó.
– Phần cây con bên phải của một node nào đó chỉ chứa các nodes có key (giá trị/data) lớn hơn key của node đó.
– Mỗi phần cây con bên trái và phần cây con bên phải cũng phải là một Binary Search Tree. Không được có các nodes trùng lặp.
Các tính chất trên của Binary Search Tree cung cấp một thứ tự sắp xếp áp dụng lên các nodes, để cho các thao tác tìm kiếm, tìm giá trị nhỏ nhất, tìm giá trị lớn nhất có thể được thực hiện nhanh chóng. Nếu không có thứ tự nào áp dụng lên các nodes, chúng ta có thể sẽ phải so sánh mọi keys để tìm kiếm một key cụ thể.
Nội dung chính
1. Tìm kiếm một key
Để tìm kiếm một giá trị, nếu đã có một mảng đã được sắp xếp, chúng ta có thể thực hiện tìm kiếm nhị phân (binary search). Giả sử chúng ta muốn tìm kiếm một số ở trong mảng, khi thực hiện điều này bằng tìm kiếm nhị phân, trước tiên chúng ta sẽ xác định toàn bộ mảng này là không gian tìm kiếm, và số cần tìm chỉ có thể tồn tại bên trong không gian tìm kiếm này. Tiếp theo, chúng ta sẽ so sánh số cần tìm/phần tử cần tìm với phần tử nằm ở giữa không gian tìm kiếm hoặc hoặc với số trung vị (median), và nếu giá trị cần tìm là nhỏ hơn, chúng ta sẽ tiếp tục tìm kiếm ở nửa bên trái của mảng, ngược lại chúng ta sẽ tiếp tục tìm kiếm ở nửa bên phải của mảng; trong trường hợp bằng nhau, lúc này chúng ta đã tìm thấy phần tử cần tìm rồi. Trong tìm kiếm nhị phân, chúng ta bắt đầu với ‘n’ phần tử trong không gian tìm kiếm, và sau đó nếu phần tử giữa không phải là phần tử đang cần tìm, chúng ta sẽ giảm không gian tìm kiếm thành ‘n/2’ và tiếp tục giảm kích thước không gian tìm kiếm cho đến khi hoặc là tìm thấy giá trị đang cần tìm, hoặc là cho đến khi chỉ còn một phần tử duy nhất ở trong không gian tìm kiếm và lúc này tìm kiếm kết thúc mà không tìm thấy giá trị cần tìm.
Thao tác tìm kiếm ở trong Binary Search Tree cũng sẽ tương tự như vậy. giả sử, chúng ta muốn tìm kiếm một số cụ thể, chúng ta sẽ bắt đầu tìm kiếm từ node root và sau đó so sánh giá trị cần tìm với giá trị của node root, nếu chúng bằng nhau tức là ta đã tìm thấy phần tử mong muốn, và quá trình tìm kiếm kết thúc; nếu giá trị cần tìm nhỏ hơn giá trị của node root, chúng ta cần tiếp tục việc tìm kiếm ở phần cây con bên trái bởi vì trong một Binary Search Tree thì tất cả các phần tử nằm trong phần cây con bên trái đều nhỏ hơn và tất cả các phần tử nằm trong phần cây con bên phải đều lớn hơn. Việc tìm kiếm một phần tử trong Binary Search Tree về cơ bản chính là quá trình duyệt/tìm kiếm này, trong đó ở mỗi bước chúng ta sẽ đi tiếp hoặc là theo hướng sang trái hoặc là sang phải, và do đó ở mỗi bước, chúng ta sẽ loại trừ được một trong các phần cây con của cây ban đầu. Nếu cây ban đầu đã được cân bằng rồi, chúng ta coi một cây là đã được cân bằng khi sự khác biệt giữa chiều cao của phần cây con bên trái và phần cây con bên phải không lớn hơn một, chúng ta sẽ bắt đầu với một không gian tìm kiếm gồm ‘n’ nodes và bất cứ khi nào chúng ta loại bỏ một trong các phần cây con, điều này cũng đồng nghĩa với chúng ta loại bỏ đi ‘n/2’ nodes khỏi không gian tìm kiếm, tức là khi đó không gian tìm kiếm của chúng ta sẽ giảm xuống còn ‘n/2’ và sau đó trong bước tiếp theo chúng ta sẽ giảm không gian tìm kiếm xuống thành ‘n/4’ và chúng ta sẽ tiếp tục giảm kích thước của không gian tìm kiếm như vậy cho đến khi tìm thấy phần tử mong muốn, hoặc cho đến khi không gian tìm kiếm giảm xuống chỉ còn một node. Quá trình tìm kiếm ở đây chính là một tìm kiếm nhị phân, và đó là lý do vì sao cái tên Binary Search Tree – Cây tìm kiếm nhị phân xuất hiện.
Sau đây sẽ là các đoạn code ví dụ cài đặt thao tác tìm kiếm một key cụ thể ở trong một Binary Search Tree được cho:
Tìm kiếm một key cụ thể trong một BST bằng C/C++:
// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
Tìm kiếm một key cụ thể trong một BST bằng Java:
// A utility function to search a given key in BST
public Node search(Node root, int key)
{
// Base Cases: root is null or key is present at root
if (root==null || root.key==key)
return root;
// val is greater than root's key
if (root.key > key)
return search(root.left, key);
// val is less than root's key
return search(root.right, key);
}
Tìm kiếm một key cụ thể trong một BST bằng Python:
# A utility function to search a given key in BST
def search(root,key):
# Base Cases: root is null or key is present at root
if root is None or root.val == key:
return root
# Key is greater than root's key
if root.val < key:
return search(root.right,key)
# Key is smaller than root's key
return search(root.left,key)
Ví dụ minh họa tìm kiếm key có giá trị 6 trong cây bên dưới:
1. Bắt đầu từ node root
2. So sánh giá trị muốn tìm với giá trị của node root, nếu nhỏ hơn root thì tiếp tục đệ quy cho phần cây con bên trái của cây ban đầu, ngược lại, nếu lớn hơn root thì đệ quy với phần cây con bên phải của cây.
3. Nếu phần tử cần tìm được tìm thấy thì return true, ngược lại return false.
2. Chèn thêm một key vào BST
Một key mới sẽ luôn luôn được chèn vào BST dưới dạng một node lá. Chúng ta sẽ bắt đầu tìm kiếm từ node root cho đến khi gặp được một node lá. Khi tìm thấy một node lá, node mới sẽ được chèn thêm vào BST làm node con của node lá này.
100 100
/ \ Insert 40 / \
20 500 ———> 20 500
/ \ / \
10 30 10 30
\
40
Sau đây sẽ là các đoạn code ví dụ cài đặt thao tác chèn thêm một key mới vào trong một Binary Search Tree được cho:
Chèn thêm node mới vào BST bằng ngôn ngữ C:
// C program to demonstrate insert operation in binary search tree.
#include<stdio.h>
#include<stdlib.h>
struct node
{
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// A utility function to do inorder traversal of BST
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
// Driver Program to test above functions
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// print inoder traversal of the BST
inorder(root);
return 0;
}
Chèn thêm node mới vào BST bằng ngôn ngữ C++:
// C++ program to demonstrate insertion
// in a BST recursively.
#include <iostream>
using namespace std;
class BST
{
int data;
BST *left, *right;
public:
// Default constructor.
BST();
// Parameterized constructor.
BST(int);
// Insert function.
BST* Insert(BST *, int);
// Inorder traversal.
void Inorder(BST *);
};
// Default Constructor definition.
BST :: BST() : data(0), left(NULL), right(NULL){}
// Parameterized Constructor definition.
BST :: BST(int value)
{
data = value;
left = right = NULL;
}
// Insert function definition.
BST* BST :: Insert(BST *root, int value)
{
if(!root)
{
// Insert the first node, if root is NULL.
return new BST(value);
}
// Insert data.
if(value > root->data)
{
// Insert right node data, if the 'value'
// to be inserted is greater than 'root' node data.
// Process right nodes.
root->right = Insert(root->right, value);
}
else
{
// Insert left node data, if the 'value'
// to be inserted is greater than 'root' node data.
// Process left nodes.
root->left = Insert(root->left, value);
}
// Return 'root' node, after insertion.
return root;
}
// Inorder traversal function.
// This gives data in sorted order.
void BST :: Inorder(BST *root)
{
if(!root)
{
return;
}
Inorder(root->left);
cout << root->data << endl;
Inorder(root->right);
}
// Driver code
int main()
{
BST b, *root = NULL;
root = b.Insert(root, 50);
b.Insert(root, 30);
b.Insert(root, 20);
b.Insert(root, 40);
b.Insert(root, 70);
b.Insert(root, 60);
b.Insert(root, 80);
b.Inorder(root);
return 0;
}
Chèn thêm node mới vào BST bằng ngôn ngữ Java:
// Java program to demonstrate insert operation in binary search tree
class BinarySearchTree {
/* Class containing left and right child of current node and key value*/
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
// Root of BST
Node root;
// Constructor
BinarySearchTree() {
root = null;
}
// This method mainly calls insertRec()
void insert(int key) {
root = insertRec(root, key);
}
/* A recursive function to insert a new key in BST */
Node insertRec(Node root, int key) {
/* If the tree is empty, return a new node */
if (root == null) {
root = new Node(key);
return root;
}
/* Otherwise, recur down the tree */
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
/* return the (unchanged) node pointer */
return root;
}
// This method mainly calls InorderRec()
void inorder() {
inorderRec(root);
}
// A utility function to do inorder traversal of BST
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.println(root.key);
inorderRec(root.right);
}
}
// Driver Program to test above functions
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
// print inorder traversal of the BST
tree.inorder();
}
}
Chèn thêm node mới vào BST bằng ngôn ngữ Python:
# Python program to demonstrate insert operation in binary search tree
# A utility class that represents an individual node in a BST
class Node:
def __init__(self,key):
self.left = None
self.right = None
self.val = key
# A utility function to insert a new node with the given key
def insert(root,key):
if root is None:
return Node(key)
else:
if root.val == key:
return root
elif root.val < key:
root.right = insert(root.right, key)
else:
root.left = insert(root.left, key)
return root
# A utility function to do inorder tree traversal
def inorder(root):
if root:
inorder(root.left)
print(root.val)
inorder(root.right)
# Driver program to test the above functions
# Let us create the following BST
# 50
# / \
# 30 70
# / \ / \
# 20 40 60 80
r = Node(50)
r = insert(r, 30)
r = insert(r, 20)
r = insert(r, 40)
r = insert(r, 70)
r = insert(r, 60)
r = insert(r, 80)
# Print inoder traversal of the BST
inorder(r)
Kết quả in ra là:
20
30
40
50
60
70
80
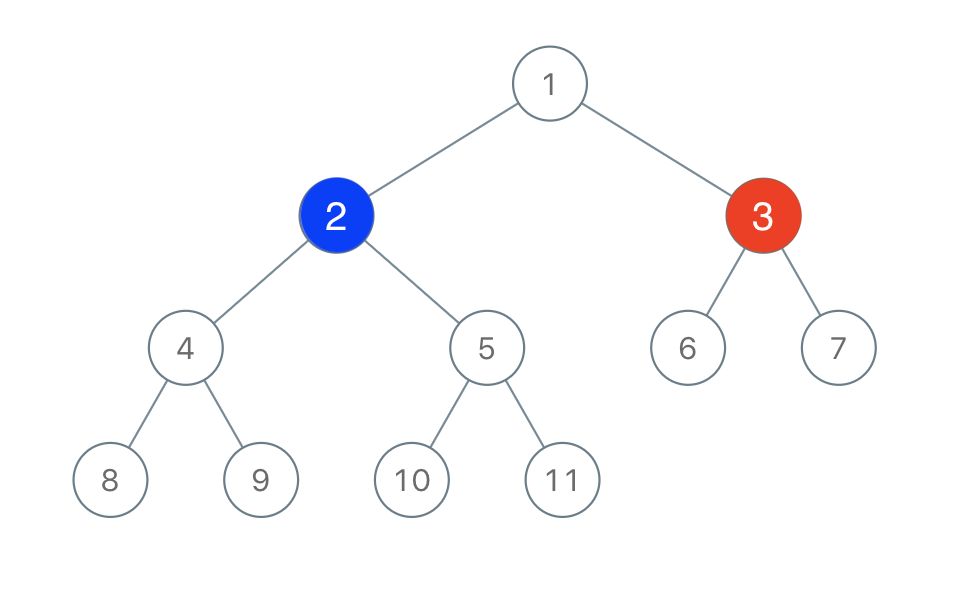
Ví dụ minh họa chèn thêm node có giá trị 2 vào cây bên dưới:
1. Bắt đầu từ node root
2. So sánh giá trị của node mới với giá trị của node root, nếu nhỏ hơn root thì tiếp tục đệ quy cho phần cây con bên trái của cây ban đầu, ngược lại, nếu lớn hơn root thì đệ quy với phần cây con bên phải của cây
3. Sau khi đi đến cuối của cây, chỉ cần chèn node mới vào bên trái (nếu node mới có giá trị nhỏ hơn node hiện tại), ngược lại, chèn node mới vào bên phải của node hiện tại.
Độ phức tạp về thời gian:
Độ phức tạp về thời gian trong trường hợp xấu nhất của thao tác tìm kiếm và chèn thêm node mới là O(h), trong đó h là chiều cao của Binary Search Tree. Trong trường hợp xấu nhất này, chúng ta có thể phải duyệt từ node root cho đến node lá sâu nhất của cây. Chiều cao của một cây lệch (skewed tree) có thể trở thành n, và độ phức tạp về thời gian của thao tác tìm kiếm và chèn thêm node mới có thể trở thành O(n).
Một số sự thật thú vị:
– Việc duyệt Binary Search Tree theo thứ tự luôn luôn tạo ra các output đã được sắp xếp.
– Chúng ta có thể xây dựng một Binary Search Tree bằng một trong kiểu duyệt cây Pre-order (Duyệt cây thứ tự trước, theo kiểu Node -> Left -> Right), Pos-order (Duyệt cây thứ tự sau, theo kiểu Left -> Right -> Node), hoặc Level Order (Duyệt cây thứ tự tầng, đi qua lần lượt từng tầng của Binary Search Tree).
– Với n khóa/n giá trị riêng biệt, Số lượng các cây Binary Search Trees độc nhất là Số Catalan.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
 và giải thuật, sau đây cafedev sẽ giới thiệu và chia sẻ chi){kind=link}