Chào ace, bài này chúng ta sẽ tìm hiểu về Cài đặt Queue bằng cách sử dụng Stack trong series tự học về cấu trúc dữ liệu(CTDL) và giải thuật, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, độ phức tạp, ứng dụng của nó, code ví dụ…) về nó thông qua các phần sau.
Trong bài học này chúng ta sẽ tìm hiểu về một bài toán, đó là: Cho trước một cấu trúc dữ liệu Stack với các thao tác xử lý dữ liệu là Push (đẩy thêm phần tử mới vào Stack) và Pop (Đưa phần tử nằm ở đỉnh Stack ra ngoài), nhiệm vụ cần làm là hãy cài đặt một cấu trúc dữ liệu Queue – Hàng đợi bằng cách sử dụng các thể hiện của cấu trúc dữ liệu Stack được cho ở trên, và hai thao tác xử lý dữ liệu đi kèm.
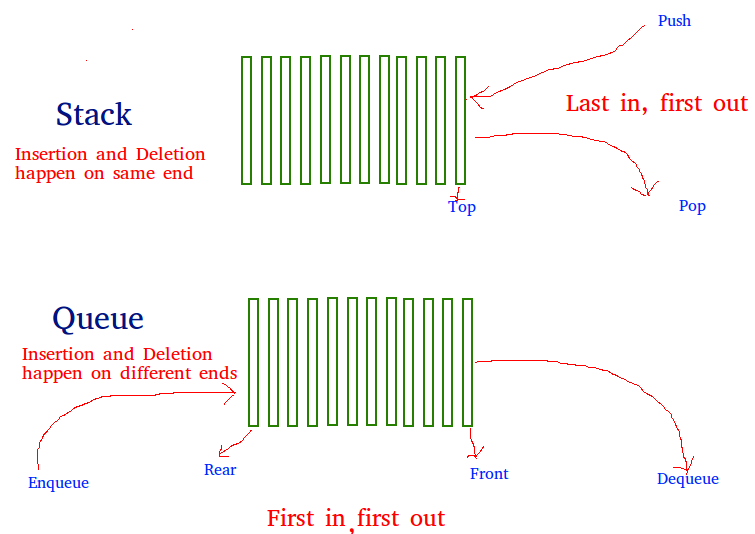
Có thể cài đặt một Queue – Hàng đợi bằng cách sử dụng hai Stacks – Ngăn xếp. Gọi Queue sẽ được cài đặt là q và các Stacks được sử dụng để cài đặt q là stack1 và stack2. q có thể được cài đặt theo hai phương pháp:
Nội dung chính
1. Phương pháp 1 – Bằng cách làm cho thao tác enQueue trở nên tốn kém
Cách này sẽ đảm bảo rằng phần tử được chèn vào muộn nhất sẽ luôn luôn nằm ở đỉnh của stack1, nhờ vậy, thao tác deQueue lúc này sẽ chỉ là lấy ra phần tử từ stack1. stack2 sẽ được sử dụng để chèn thêm phần tử mới vào đỉnh của stack1
enQueue(q, x):
– Trong khi stack1 không trống, đẩy mọi phần tử từ stack1 sang stack2
– Đẩy x vào stack1 (giả sử kích thước của stack1 và stack2 là vô hạn)
– Đẩy mọi phần tử từ stack2 trở về stack1.
Độ phức tạp về thời gian của hàm enQueue trong phương pháp 1 này là O(n)
deQueue(q):
– Nếu stack1 là trống (empty) -> lỗi
– Ngược lại, đẩy một phần tử ở đỉnh stack1 ra ngoài, và return (trả về) phần tử đó.
Độ phức tạp về thời gian của hamde deQueue trong phương pháp 1 này là O(1)
Sau đây sẽ là các đoạn code ví dụ cài đặt phương pháp 1 trong chủ đề cài đặt Queue bằng cách sử dụng Stack.
CÁC ĐOẠN CODE VÍ DỤ ĐƯỢC VIẾT BẰNG C++ JAVA PYTHON3 C#
C++
// CPP program to implement Queue using
// two stacks with costly enQueue()
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
void enQueue(int x)
{
// Move all elements from s1 to s2
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
// Push item into s1
s1.push(x);
// Push everything back to s1
while (!s2.empty()) {
s1.push(s2.top());
s2.pop();
}
}
// Dequeue an item from the queue
int deQueue()
{
// if first stack is empty
if (s1.empty()) {
cout << "Q is Empty";
exit(0);
}
// Return top of s1
int x = s1.top();
s1.pop();
return x;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
Java
// Java program to implement Queue using
// two stacks with costly enQueue()
import java.util.*;
class GFG
{
static class Queue
{
static Stack<Integer> s1 = new Stack<Integer>();
static Stack<Integer> s2 = new Stack<Integer>();
static void enQueue(int x)
{
// Move all elements from s1 to s2
while (!s1.isEmpty())
{
s2.push(s1.pop());
//s1.pop();
}
// Push item into s1
s1.push(x);
// Push everything back to s1
while (!s2.isEmpty())
{
s1.push(s2.pop());
//s2.pop();
}
}
// Dequeue an item from the queue
static int deQueue()
{
// if first stack is empty
if (s1.isEmpty())
{
System.out.println("Q is Empty");
System.exit(0);
}
// Return top of s1
int x = s1.peek();
s1.pop();
return x;
}
};
// Driver code
public static void main(String[] args)
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
System.out.println(q.deQueue());
System.out.println(q.deQueue());
System.out.println(q.deQueue());
}
}
Python
# Python3 program to implement Queue using
# two stacks with costly enQueue()
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
def enQueue(self, x):
# Move all elements from s1 to s2
while len(self.s1) != 0:
self.s2.append(self.s1[-1])
self.s1.pop()
# Push item into self.s1
self.s1.append(x)
# Push everything back to s1
while len(self.s2) != 0:
self.s1.append(self.s2[-1])
self.s2.pop()
# Dequeue an item from the queue
def deQueue(self):
# if first stack is empty
if len(self.s1) == 0:
print("Q is Empty")
# Return top of self.s1
x = self.s1[-1]
self.s1.pop()
return x
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue()) C#
// C# program to implement Queue using
// two stacks with costly enQueue()
using System;
using System.Collections;
class GFG
{
public class Queue
{
public Stack s1 = new Stack();
public Stack s2 = new Stack();
public void enQueue(int x)
{
// Move all elements from s1 to s2
while (s1.Count > 0)
{
s2.Push(s1.Pop());
//s1.Pop();
}
// Push item into s1
s1.Push(x);
// Push everything back to s1
while (s2.Count > 0)
{
s1.Push(s2.Pop());
//s2.Pop();
}
}
// Dequeue an item from the queue
public int deQueue()
{
// if first stack is empty
if (s1.Count == 0)
{
Console.WriteLine("Q is Empty");
}
// Return top of s1
int x = (int)s1.Peek();
s1.Pop();
return x;
}
};
// Driver code
public static void Main()
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue());
}
} Kết quả in ra là:
1
2
3Phân tích độ phức tạp:
– Độ phức tạp về thời gian:
+ Thao tác Push (đẩy thêm phần tử mới vào Queue): O(N)
Trong trường hợp xấu nhất, cả stack1 và stack2 đều trống (empty).
+ Thao tác Pop (đưa/lấy phần tử ra khỏi Queue): O(1)
Giống với thao tác Pop trong Stack.
– Độ phức tạp về không gian: O(N).
Sử dụng Stack để lưu các giá trị.
2. Phương pháp 2 – Bằng cách làm cho thao tác deQueue trở nên tốn kém
Trong phương pháp này, khi thực hiện thao tác enQueue, phần tử mới sẽ được chèn vào đỉnh của stack1. Còn khi thực hiện thao tác deQueue, nếu stack2 là trống, vậy thì tất cả các phần tử sẽ được di chuyển sang stack2 và cuối cùng, phần tử nằm ở đỉnh stack2 sẽ được return (trả về).
enQueue(q, x):
– Đẩy x vào stack1 (giả sử kích thước của stack1 và stack2 là vô hạn). Tại đây, độ phức tạp về thời gian sẽ là O(1).
deQueue(q):
– Nếu stack1 và stack2 đều trống -> lỗi
– Nếu stack2 là trống (empty):
+ Trong khi stack1 vẫn còn phần tử (tức là stack1 chưa trống – chưa empty), đẩy mọi phần tử từ stack1 sang stack2
– Lấy ra phần tử nằm ở đỉnh stack2 và return (trả về) phần tử đó.
Tại đây, độ phức tạp về thời gian sẽ là O(n).
Phương pháp 2 chắc chắn tốt hơn phương pháp 1:
– Phương pháp 1 thực hiện di chuyển tất cả các phần tử 2 lần khi thực hiện thao tác enQueue,
– Trong khi thao tác deQueue của Phương pháp 2 chỉ thực hiện di chuyển các phần tử một lần, và chỉ tiến hành di chuyển các phần tử khi stack2 đang empty – trống. Vì vậy, độ phức tạp khấu hao (amortized complexity) của thao tác dequeue sẽ trở thành O(1).
Sau đây sẽ là các đoạn code ví dụ cài đặt phương pháp 2 trong chủ đề cài đặt Queue bằng cách sử dụng Stack.
CÁC ĐOẠN CODE VÍ DỤ ĐƯỢC VIẾT BẰNG C++ C JAVA PYTHON3 C#
C
/* C Program to implement a queue using two stacks */
#include <stdio.h>
#include <stdlib.h>
/* structure of a stack node */
struct sNode {
int data;
struct sNode* next;
};
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data);
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref);
/* structure of queue having two stacks */
struct queue {
struct sNode* stack1;
struct sNode* stack2;
};
/* Function to enqueue an item to queue */
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
/* Function to deQueue an item from queue */
int deQueue(struct queue* q)
{
int x;
/* If both stacks are empty then error */
if (q->stack1 == NULL && q->stack2 == NULL) {
printf("Q is empty");
getchar();
exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q->stack2 == NULL) {
while (q->stack1 != NULL) {
x = pop(&q->stack1);
push(&q->stack2, x);
}
}
x = pop(&q->stack2);
return x;
}
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data)
{
/* allocate node */
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*top_ref);
/* move the head to point to the new node */
(*top_ref) = new_node;
}
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
/*If stack is empty then error */
if (*top_ref == NULL) {
printf("Stack underflow \n");
getchar();
exit(0);
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
/* Driver function to test anove functions */
int main()
{
/* Create a queue with items 1 2 3*/
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
q->stack2 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
C++
// CPP program to implement Queue using
// two stacks with costly deQueue()
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
// Enqueue an item to the queue
void enQueue(int x)
{
// Push item into the first stack
s1.push(x);
}
// Dequeue an item from the queue
int deQueue()
{
// if both stacks are empty
if (s1.empty() && s2.empty()) {
cout << "Q is empty";
exit(0);
}
// if s2 is empty, move
// elements from s1
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
// return the top item from s2
int x = s2.top();
s2.pop();
return x;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
Java
/* Java Program to implement a queue using two stacks */
// Note that Stack class is used for Stack implementation
import java.util.Stack;
public class GFG {
/* class of queue having two stacks */
static class Queue {
Stack<Integer> stack1;
Stack<Integer> stack2;
}
/* Function to push an item to stack*/
static void push(Stack<Integer> top_ref, int new_data)
{
// Push the data onto the stack
top_ref.push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<Integer> top_ref)
{
/*If stack is empty then error */
if (top_ref.isEmpty()) {
System.out.println("Stack Underflow");
System.exit(0);
}
// pop the data from the stack
return top_ref.pop();
}
// Function to enqueue an item to the queue
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x;
/* If both stacks are empty then error */
if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
System.out.println("Q is empty");
System.exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q.stack2.isEmpty()) {
while (!q.stack1.isEmpty()) {
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
/* Driver function to test above functions */
public static void main(String args[])
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<>();
q.stack2 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.println(deQueue(q) + " ");
}
} Python3
# Python3 program to implement Queue using
# two stacks with costly deQueue()
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
# EnQueue item to the queue
def enQueue(self, x):
self.s1.append(x)
# DeQueue item from the queue
def deQueue(self):
# if both the stacks are empty
if len(self.s1) == 0 and len(self.s2) == 0:
print("Q is Empty")
return
# if s2 is empty and s1 has elements
elif len(self.s2) == 0 and len(self.s1) > 0:
while len(self.s1):
temp = self.s1.pop()
self.s2.append(temp)
return self.s2.pop()
else:
return self.s2.pop()
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue()) C#
/* C# Program to implement a queue using two stacks */
// Note that Stack class is used for Stack implementation
using System;
using System.Collections.Generic;
class GFG
{
/* class of queue having two stacks */
public class Queue
{
public Stack<int> stack1;
public Stack<int> stack2;
}
/* Function to push an item to stack*/
static void push(Stack<int> top_ref, int new_data)
{
// Push the data onto the stack
top_ref.Push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<int> top_ref)
{
/*If stack is empty then error */
if (top_ref.Count == 0)
{
Console.WriteLine("Stack Underflow");
Environment.Exit(0);
}
// pop the data from the stack
return top_ref.Pop();
}
// Function to enqueue an item to the queue
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x;
/* If both stacks are empty then error */
if (q.stack1.Count == 0 && q.stack2.Count == 0)
{
Console.WriteLine("Q is empty");
Environment.Exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q.stack2.Count == 0)
{
while (q.stack1.Count != 0)
{
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
/* Driver code */
public static void Main(String []args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<int>();
q.stack2 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.WriteLine(deQueue(q) + " ");
}
} Kết quả in ra là:
1 2 3 Phân tích độ phức tạp:
– Độ phức tạp về thời gian:
+ Thao tác Push (đẩy thêm phần tử mới vào Queue): O(1)
Giống với thao tác Pop trong Stack.
+ Thao tác Pop (lấy phần tử ra khỏi Queue): O(N)
Trong trường hợp xấu nhất, cả stack1 và stack2 đều trống – empty.
– Độ phức tạp về không gian: O(N)
Sử dụng Stack để lưu các giá trị.
Queue cũng có thể được cài đặt bằng cách sử dụng một user stack (ngăn xếp dành cho người dùng sử dụng) và một Fuction Call Stack (ngăn xếp gọi hàm). Phần sau đây sẽ mô tả Phương pháp 2 đã được chỉnh sửa, trong đó đệ quy (hay chính là Function Call Stack) sẽ được sử dụng để cài đặt Queue sao cho chỉ cần sử dụng một stack do người dùng định nghĩa.
enQueue(x):
– Đẩy x vào stack1.
deQueue:
– Nếu stack1 là trống – empty -> lỗi
– Nếu stack1 chỉ có một phần tử, vậy thì return – trả về phần tử đó luôn
– Sử dụng đệ quy để lấy ra mọi phần tử khỏi stack1, lưu lại mỗi phần tử được lấy ra vào trong một biến res, đẩy lại res vào stack1, rồi trả về res.
Bước thứ 3 – bước cuối cùng để đảm bảo rằng phần tử cuối cùng được lấy ra khỏi Queue sẽ luôn luôn được trả về (returned), và bởi vì đệ quy sẽ dừng khi chỉ có duy nhất 1 phần tử nằm trong stack1 (bước thứ 2), chúng ta lấy ra phần tử cuối cùng của stack1 trong hàm deQueue() và tất cả các phần tử khác được đẩy trở lại vào stack1 trong bước 3.
3. Cài đặt phương pháp 2 bằng cách sử dụng Function Call Stack
CÁC ĐOẠN CODE VÍ DỤ ĐƯỢC VIẾT BẰNG C++ C JAVA C# PYTHON3
C
/* Program to implement a queue using one user defined stack
and one Function Call Stack */
#include <stdio.h>
#include <stdlib.h>
/* structure of a stack node */
struct sNode {
int data;
struct sNode* next;
};
/* structure of queue having two stacks */
struct queue {
struct sNode* stack1;
};
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data);
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref);
/* Function to enqueue an item to queue */
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
/* Function to deQueue an item from queue */
int deQueue(struct queue* q)
{
int x, res;
/* If both stacks are empty then error */
if (q->stack1 == NULL) {
printf("Q is empty");
getchar();
exit(0);
}
else if (q->stack1->next == NULL) {
return pop(&q->stack1);
}
else {
/* pop an item from the stack1 */
x = pop(&q->stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(&q->stack1, x);
return res;
}
}
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data)
{
/* allocate node */
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*top_ref);
/* move the head to point to the new node */
(*top_ref) = new_node;
}
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
/*If stack is empty then error */
if (*top_ref == NULL) {
printf("Stack underflow \n");
getchar();
exit(0);
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
/* Driver function to test above functions */
int main()
{
/* Create a queue with items 1 2 3*/
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
C++
// CPP program to implement Queue using
// one stack and recursive call stack.
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s;
// Enqueue an item to the queue
void enQueue(int x)
{
s.push(x);
}
// Dequeue an item from the queue
int deQueue()
{
if (s.empty()) {
cout << "Q is empty";
exit(0);
}
// pop an item from the stack
int x = s.top();
s.pop();
// if stack becomes empty, return
// the popped item
if (s.empty())
return x;
// recursive call
int item = deQueue();
// push popped item back to the stack
s.push(x);
// return the result of deQueue() call
return item;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
Java
// Java Program to implement a queue using one stack
import java.util.Stack;
public class QOneStack {
// class of queue having two stacks
static class Queue {
Stack<Integer> stack1;
}
/* Function to push an item to stack*/
static void push(Stack<Integer> top_ref, int new_data)
{
/* put in the data */
top_ref.push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<Integer> top_ref)
{
/*If stack is empty then error */
if (top_ref == null) {
System.out.println("Stack Underflow");
System.exit(0);
}
// return element from stack
return top_ref.pop();
}
/* Function to enqueue an item to queue */
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x, res = 0;
/* If the stacks is empty then error */
if (q.stack1.isEmpty()) {
System.out.println("Q is Empty");
System.exit(0);
}
// Check if it is a last element of stack
else if (q.stack1.size() == 1) {
return pop(q.stack1);
}
else {
/* pop an item from the stack1 */
x = pop(q.stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(q.stack1, x);
return res;
}
return 0;
}
/* Driver function to test above functions */
public static void main(String[] args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
}
} Python3
# Python3 program to implement Queue using
# one stack and recursive call stack.
class Queue:
def __init__(self):
self.s = []
# Enqueue an item to the queue
def enQueue(self, data):
self.s.append(data)
# Dequeue an item from the queue
def deQueue(self):
# Return if queue is empty
if len(self.s) <= 0:
print('Queue is empty')
return
# pop an item from the stack
x = self.s[len(self.s) - 1]
self.s.pop()
# if stack become empty
# return the popped item
if len(self.s) <= 0:
return x
# recursive call
item = self.deQueue()
# push popped item back to
# the stack
self.s.append(x)
# return the result of
# deQueue() call
return item
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
C#
// C# Program to implement a queue using one stack
using System;
using System.Collections.Generic;
public class QOneStack
{
// class of queue having two stacks
public class Queue
{
public Stack<int> stack1;
}
/* Function to push an item to stack*/
static void push(Stack<int> top_ref, int new_data)
{
/* put in the data */
top_ref.Push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<int> top_ref)
{
/*If stack is empty then error */
if (top_ref == null)
{
Console.WriteLine("Stack Underflow");
Environment.Exit(0);
}
// return element from stack
return top_ref.Pop();
}
/* Function to enqueue an item to queue */
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x, res = 0;
/* If the stacks is empty then error */
if (q.stack1.Count == 0)
{
Console.WriteLine("Q is Empty");
Environment.Exit(0);
}
// Check if it is a last element of stack
else if (q.stack1.Count == 1)
{
return pop(q.stack1);
}
else
{
/* pop an item from the stack1 */
x = pop(q.stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(q.stack1, x);
return res;
}
return 0;
}
/* Driver function to test above functions */
public static void Main(String[] args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
}
}
Kết quả in ra là:
1 2 3Phân tích độ phức tạp:
– Độ phức tạp về thời gian:
+ Thao tác Push (chèn thêm phần tử mới vào Queue): O(1)
Giống với thao tác Pop (lấy ra phần tử ở đỉnh ngăn xếp) trong Stack
+ Thao tác Pop (lấy phần tử ra khỏi Queue): O(N)
Sự khác biệt giữa Phương pháp 2 được chỉnh sửa và Phương pháp 2 thuần túy đó là, trong thao tác Pop của Phương pháp 2 được chỉnh sửa, một phần tử cụ thể sẽ được trả về và tất cả các phần tử sẽ được lưu trữ trở lại vào trong một lời gọi hàm duy nhất.
– Độ phức tạp về không gian: O(N)
Sử dụng Stack để lưu các giá trị.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!



![[CTDL] Tìm node có giá trị nhỏ nhất trong Binary Search Tree](https://cafedev.vn/wp-content/uploads/2020/07/cafedev-binary-tree-coloring-game-218x150.png)



![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

