Tiếp theo bài trước, bài này chúng ta sẽ tìm hiểu về việc Phân tích tiệm cận(Asymptotic analysis) của một thuật toán, tại sao chúng ta phải làm điều này.
Nội dung chính
1. Khái niệm
Phân tích tiệm cận của một thuật toán đề cập đến việc xác định giới hạn / khung toán học đối với hiệu suất thời gian chạy của nó. Sử dụng phân tích tiệm cận, chúng ta rất có thể kết luận trường hợp tốt nhất, trường hợp trung bình và trường hợp xấu nhất của một thuật toán.
Phân tích tiệm cận bị ràng buộc đầu vào, tức là nếu không có đầu vào cho thuật toán, nó được kết luận là hoạt động trong một thời gian không đổi. Ngoài “đầu vào” tất cả các yếu tố khác được coi là không đổi.
Phân tích tiệm cận đề cập đến việc tính toán thời gian chạy của bất kỳ hoạt động nào trong các đơn vị tính toán. Ví dụ, thời gian chạy của một hoạt động được tính là f (n) và có thể đối với một hoạt động khác, nó được tính là g (n2). Điều này có nghĩa là thời gian chạy hoạt động đầu tiên sẽ tăng tuyến tính với sự gia tăng của n và thời gian chạy của hoạt động thứ hai sẽ tăng theo cấp số nhân khi n tăng. Tương tự, thời gian chạy của cả hai hoạt động sẽ gần như nhau nếu n nhỏ hơn đáng kể.
Thông thường, thời gian theo yêu cầu của một thuật toán thuộc ba loại:
- Trường hợp tốt nhất(Best Case) – Thời gian tối thiểu cần thiết để thực hiện chương trình.
- Trường hợp trung bình(Average Case ) – Thời gian trung bình cần thiết để thực hiện chương trình.
- Trường hợp xấu nhất(Worst Case) – Thời gian tối đa cần thiết để thực hiện chương trình.
2. Ký hiệu tiệm cận
Sau đây là các ký hiệu tiệm cận thường được sử dụng để tính độ phức tạp thời gian chạy của một thuật toán.
- Ký hiệu O
- Ký hiệu Ω
- Kí hiệu θ
Ký hiệu Big Oh, Ο
Kí hiệu Ο (n) là cách chính thức để biểu thị giới hạn trên của thời gian chạy thuật toán. Nó đo độ phức tạp thời gian trong trường hợp xấu nhất hoặc khoảng thời gian dài nhất mà một thuật toán có thể mất để hoàn thành.
Kí hiệu Omega, Ω
Kí hiệu Ω (n) là cách chính thức để biểu thị giới hạn dưới của thời gian chạy thuật toán. Nó đo lường độ phức tạp thời gian của trường hợp tốt nhất hoặc khoảng thời gian tốt nhất mà một thuật toán có thể có để hoàn thành.
Ký hiệu Theta, θ
Kí hiệu θ (n) là cách chính thức để biểu thị cả giới hạn dưới và giới hạn trên của thời gian chạy thuật toán. Nó được biểu diễn như sau:
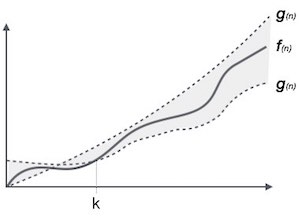
3. Các ký hiệu tiệm cận phổ biến
Sau đây là danh sách một số ký hiệu tiệm cận phổ biến
| constant(hằng) | – | Ο(1) |
| logarithmic | – | Ο(log n) |
| linear(tuyến tính) | – | Ο(n) |
| n log n | – | Ο(n log n) |
| quadratic(bậc 2) | – | Ο(n2) |
| cubic(khối) | – | Ο(n3) |
| polynomial(đa thức) | – | nΟ(1) |
| exponential(mũ số) | – | 2Ο(n) |
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
 của một thuật toán, tại sao chúng ta phải làm điều này.){kind=link}