Chào ace, bài này chúng ta sẽ tìm hiểu về một trong các thuật toán sắp xếp được sử dụng nhiều trong lập trình và thực tế nhất đó là Cycle Sort, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, ứng dụng của nó, code ví dụ, điểm mạnh, điểm yếu…) về Cycle Sort thông qua các phần sau.
Nội dung chính
1. Giới thiệu
Sắp xếp theo chu kỳ(Cycle Sort) là một Thuật toán sắp xếp tại chỗ, thuật toán sắp xếp không ổn định, một sắp xếp so sánh tối ưu về mặt lý thuyết về tổng số lần ghi vào mảng ban đầu.
Nó là tối ưu về số lượng bộ nhớ ghi. Nó giảm thiểu số lượng bộ nhớ ghi để sắp xếp (Mỗi giá trị hoặc được ghi 0 lần, nếu nó đã ở đúng vị trí của nó hoặc được ghi một lần vào đúng vị trí của nó.)
Nó dựa trên ý tưởng rằng mảng được sắp xếp có thể được chia thành các chu kỳ. Các chu kỳ có thể được hình dung dưới dạng đồ thị. Chúng ta có n nút và một cạnh được hướng từ nút i đến nút j nếu phần tử ở chỉ mục thứ i phải có mặt ở chỉ mục thứ j trong mảng đã sắp xếp.
Chu kỳ trong arr [] = {2, 4, 5, 1, 3}
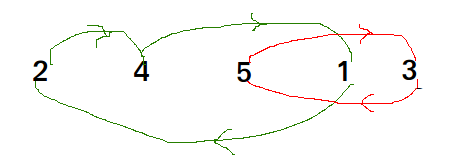
Chu kỳ trong arr [] = {4, 3, 2, 1}
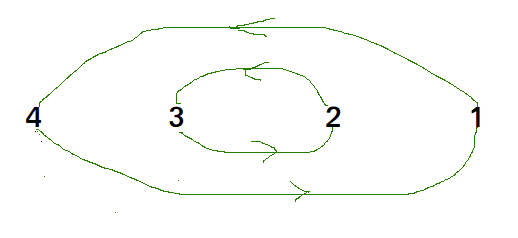
Chúng ta từng người một xem xét tất cả các chu kỳ. Đầu tiên chúng ta xem xét chu trình bao gồm phần tử đầu tiên. Chúng ta tìm đúng vị trí của phần tử đầu tiên, đặt nó vào đúng vị trí của nó, giả sử j. Chúng ta xem xét giá trị cũ của arr [j] và tìm vị trí chính xác của nó, chúng ta tiếp tục làm điều này cho đến khi tất cả các phần tử của chu kỳ hiện tại được đặt ở vị trí chính xác, tức là chúng ta không quay lại điểm bắt đầu chu kỳ.
Giải thích:
arr [] = {10, 5, 2, 3}
index = 0 1 2 3
cycle_start = 0
item = 10 = arr [0]
Tìm vị trí nơi chúng ta đặt vật phẩm
pos = cycle_start
i = pos + 1
trong khi (i <n)
if (arr [i] <item)
pos ++;
Chúng ta đặt 10 tại arr [3] và đổi item thành
giá trị cũ của arr [3].
arr [] = {10, 5, 2, 10}
item = 3
Một lần nữa xoay chu kỳ nghỉ bắt đầu bằng chỉ mục '0'
Tìm vị trí mà chúng ta item = 3
chúng ta trao đổi mục với phần tử tại arr [1] ngay bây giờ
arr [] = {10, 3, 2, 10}
item = 5
Một lần nữa xoay chu kỳ nghỉ bắt đầu với index '0' và item = 5
chúng tôi hoán đổi mục với phần tử tại arr [2].
arr [] = {10, 3, 5, 10}
item = 2
Một lần nữa xoay chu kỳ nghỉ bắt đầu với index '0' và item = 2
arr [] = {2, 3, 5, 10}
Trên đây là một lần lặp lại cho cycle_stat = 0.
Lặp lại các bước trên cho cycle_start = 1, 2, ..n-22. Code ví dụ trên nhiều ngôn ngữ
C++
// C++ program to implement cycle sort
#include <iostream>
using namespace std;
// Function sort the array using Cycle sort
void cycleSort(int arr[], int n)
{
// count number of memory writes
int writes = 0;
// traverse array elements and put it to on
// the right place
for (int cycle_start = 0; cycle_start <= n - 2; cycle_start++) {
// initialize item as starting point
int item = arr[cycle_start];
// Find position where we put the item. We basically
// count all smaller elements on right side of item.
int pos = cycle_start;
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos++;
// If item is already in correct position
if (pos == cycle_start)
continue;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (pos != cycle_start) {
swap(item, arr[pos]);
writes++;
}
// Rotate rest of the cycle
while (pos != cycle_start) {
pos = cycle_start;
// Find position where we put the element
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos += 1;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (item != arr[pos]) {
swap(item, arr[pos]);
writes++;
}
}
}
// Number of memory writes or swaps
// cout << writes << endl ;
}
// Driver program to test above function
int main()
{
int arr[] = { 1, 8, 3, 9, 10, 10, 2, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
cycleSort(arr, n);
cout << "After sort : " << endl;
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
Java
// Java program to implement cycle sort
import java.util.*;
import java.lang.*;
class GFG {
// Function sort the array using Cycle sort
public static void cycleSort(int arr[], int n)
{
// count number of memory writes
int writes = 0;
// traverse array elements and put it to on
// the right place
for (int cycle_start = 0; cycle_start <= n - 2; cycle_start++) {
// initialize item as starting point
int item = arr[cycle_start];
// Find position where we put the item. We basically
// count all smaller elements on right side of item.
int pos = cycle_start;
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos++;
// If item is already in correct position
if (pos == cycle_start)
continue;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (pos != cycle_start) {
int temp = item;
item = arr[pos];
arr[pos] = temp;
writes++;
}
// Rotate rest of the cycle
while (pos != cycle_start) {
pos = cycle_start;
// Find position where we put the element
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos += 1;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (item != arr[pos]) {
int temp = item;
item = arr[pos];
arr[pos] = temp;
writes++;
}
}
}
}
// Driver program to test above function
public static void main(String[] args)
{
int arr[] = { 1, 8, 3, 9, 10, 10, 2, 4 };
int n = arr.length;
cycleSort(arr, n);
System.out.println("After sort : ");
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
} Python 3
# Python program to implement cycle sort
def cycleSort(array):
writes = 0
# Loop through the array to find cycles to rotate.
for cycleStart in range(0, len(array) - 1):
item = array[cycleStart]
# Find where to put the item.
pos = cycleStart
for i in range(cycleStart + 1, len(array)):
if array[i] < item:
pos += 1
# If the item is already there, this is not a cycle.
if pos == cycleStart:
continue
# Otherwise, put the item there or right after any duplicates.
while item == array[pos]:
pos += 1
array[pos], item = item, array[pos]
writes += 1
# Rotate the rest of the cycle.
while pos != cycleStart:
# Find where to put the item.
pos = cycleStart
for i in range(cycleStart + 1, len(array)):
if array[i] < item:
pos += 1
# Put the item there or right after any duplicates.
while item == array[pos]:
pos += 1
array[pos], item = item, array[pos]
writes += 1
return writes
# driver code
arr = [1, 8, 3, 9, 10, 10, 2, 4 ]
n = len(arr)
cycleSort(arr)
print("After sort : ")
for i in range(0, n) :
print(arr[i], end = ' ') C#
// C# program to implement cycle sort
using System;
class GFG {
// Function sort the array using Cycle sort
public static void cycleSort(int[] arr, int n)
{
// count number of memory writes
int writes = 0;
// traverse array elements and
// put it to on the right place
for (int cycle_start = 0; cycle_start <= n - 2; cycle_start++)
{
// initialize item as starting point
int item = arr[cycle_start];
// Find position where we put the item.
// We basically count all smaller elements
// on right side of item.
int pos = cycle_start;
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos++;
// If item is already in correct position
if (pos == cycle_start)
continue;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (pos != cycle_start) {
int temp = item;
item = arr[pos];
arr[pos] = temp;
writes++;
}
// Rotate rest of the cycle
while (pos != cycle_start) {
pos = cycle_start;
// Find position where we put the element
for (int i = cycle_start + 1; i < n; i++)
if (arr[i] < item)
pos += 1;
// ignore all duplicate elements
while (item == arr[pos])
pos += 1;
// put the item to it's right position
if (item != arr[pos]) {
int temp = item;
item = arr[pos];
arr[pos] = temp;
writes++;
}
}
}
}
// Driver program to test above function
public static void Main()
{
int[] arr = { 1, 8, 3, 9, 10, 10, 2, 4 };
int n = arr.Length;
// Function calling
cycleSort(arr, n);
Console.Write("After sort : ");
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
} Kết quả
After sort :
1 2 3 4 8 9 10 10 3. Độ phức tạp
Độ phức tạp về thời gian: O (n2)
Trường hợp tệ nhất: O (n2)
Trường hợp Trung bình: O (n2)
Trường hợp tốt nhất: O (n2)
Thuật toán sắp xếp này phù hợp nhất cho các tình huống mà các hoạt động ghi hoặc hoán đổi bộ nhớ là tốn kém.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

