Chào ace, bài này chúng ta sẽ tìm hiểu về một trong các thuật toán sắp xếp được sử dụng nhiều trong lập trình và thực tế nhất đó là Exponential Search, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, ứng dụng của nó, code ví dụ, điểm mạnh, điểm yếu…) về Exponential Search thông qua các phần sau.
Nội dung chính
1. Giới thiệu
Tên của thuật toán tìm kiếm này có thể gây hiểu nhầm vì nó hoạt động trong thời gian O (Log n). Tên xuất phát từ cách nó tìm kiếm một phần tử.
Cho một mảng được sắp xếp và một phần tử x là đã tìm, tìm vị trí của x trong mảng.
Đầu vào: arr [] = {10, 20, 40, 45, 55}
x = 45
Đầu ra: Phần tử được tìm thấy ở chỉ mục 3
Đầu vào: arr [] = {10, 15, 25, 45, 55}
x = 15
Đầu ra: Phần tử được tìm thấy ở chỉ mục 1
Chúng ta đã thảo luận, tìm kiếm tuyến tính, tìm kiếm nhị phân cho vấn đề này.
Tìm kiếm theo cấp số nhân(Exponential Search) bao gồm hai bước:
- Tìm phạm vi nơi có phần tử
- Thực hiện tìm kiếm nhị phân trong phạm vi tìm thấy ở trên.
Làm thế nào để tìm phạm vi mà phần tử có thể có mặt?
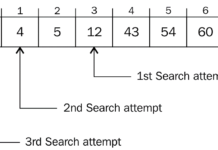
Ý tưởng là bắt đầu với kích thước mảng con 1, so sánh phần tử cuối cùng của nó với x, sau đó thử kích thước 2, rồi 4, v.v. cho đến khi phần tử cuối cùng của một mảng con không lớn hơn.
Khi chúng ta tìm thấy một chỉ số i (sau khi nhân đôi lặp lại i), chúng ta biết rằng phần tử phải có mặt giữa i / 2 và i (Tại sao lại là i / 2? Vì chúng ta không thể tìm thấy giá trị lớn hơn trong lần lặp trước)
2. Code ví dụ trên nhiều ngôn ngữ
C++
// C++ program to find an element x in a
// sorted array using Exponential search.
#include <bits/stdc++.h>
using namespace std;
int binarySearch(int arr[], int, int, int);
// Returns position of first occurrence of
// x in array
int exponentialSearch(int arr[], int n, int x)
{
// If x is present at firt location itself
if (arr[0] == x)
return 0;
// Find range for binary search by
// repeated doubling
int i = 1;
while (i < n && arr[i] <= x)
i = i*2;
// Call binary search for the found range.
return binarySearch(arr, i/2, min(i, n), x);
}
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is
// present, otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l)
{
int mid = l + (r - l)/2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then it
// can only be present n left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid-1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid+1, r, x);
}
// We reach here when element is not present
// in array
return -1;
}
// Driver code
int main(void)
{
int arr[] = {2, 3, 4, 10, 40};
int n = sizeof(arr)/ sizeof(arr[0]);
int x = 10;
int result = exponentialSearch(arr, n, x);
(result == -1)? printf("Element is not present in array")
: printf("Element is present at index %d",
result);
return 0;
}
Java
// Java program to find an element x in a
// sorted array using Exponential search.
import java.util.Arrays;
class GFG
{
// Returns position of first occurrence of
// x in array
static int exponentialSearch(int arr[],
int n, int x)
{
// If x is present at firt location itself
if (arr[0] == x)
return 0;
// Find range for binary search by
// repeated doubling
int i = 1;
while (i < n && arr[i] <= x)
i = i*2;
// Call binary search for the found range.
return Arrays.binarySearch(arr, i/2,
Math.min(i, n), x);
}
// Driver code
public static void main(String args[])
{
int arr[] = {2, 3, 4, 10, 40};
int x = 10;
int result = exponentialSearch(arr, arr.length, x);
System.out.println((result < 0) ?
"Element is not present in array" :
"Element is present at index " +
result);
}
}
Python
# Python program to find an element x
# in a sorted array using Exponential Search
# A recurssive binary search function returns
# location of x in given array arr[l..r] is
# present, otherwise -1
def binarySearch( arr, l, r, x):
if r >= l:
mid = l + ( r-l ) / 2
# If the element is present at
# the middle itself
if arr[mid] == x:
return mid
# If the element is smaller than mid,
# then it can only be present in the
# left subarray
if arr[mid] > x:
return binarySearch(arr, l,
mid - 1, x)
# Else he element can only be
# present in the right
return binarySearch(arr, mid + 1, r, x)
# We reach here if the element is not present
return -1
# Returns the position of first
# occurrence of x in array
def exponentialSearch(arr, n, x):
# IF x is present at first
# location itself
if arr[0] == x:
return 0
# Find range for binary search
# j by repeated doubling
i = 1
while i < n and arr[i] <= x:
i = i * 2
# Call binary search for the found range
return binarySearch( arr, i / 2,
min(i, n), x)
# Driver Code
arr = [2, 3, 4, 10, 40]
n = len(arr)
x = 10
result = exponentialSearch(arr, n, x)
if result == -1:
print "Element not found in thye array"
else:
print "Element is present at index %d" %(result) C#
// C# program to find an element x in a
// sorted array using Exponential search.
using System;
class GFG {
// Returns position of first
// occurrence of x in array
static int exponentialSearch(int []arr,
int n, int x)
{
// If x is present at
// first location itself
if (arr[0] == x)
return 0;
// Find range for binary search
// by repeated doubling
int i = 1;
while (i < n && arr[i] <= x)
i = i * 2;
// Call binary search for
// the found range.
return binarySearch(arr, i/2,
Math.Min(i, n), x);
}
// A recursive binary search
// function. It returns location
// of x in given array arr[l..r] is
// present, otherwise -1
static int binarySearch(int []arr, int l,
int r, int x)
{
if (r >= l)
{
int mid = l + (r - l) / 2;
// If the element is present
// at the middle itself
if (arr[mid] == x)
return mid;
// If element is smaller than
// mid, then it can only be
// present n left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only
// be present in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element
// is not present in array
return -1;
}
// Driver code
public static void Main()
{
int []arr = {2, 3, 4, 10, 40};
int n = arr.Length;
int x = 10;
int result = exponentialSearch(arr, n, x);
if (result == -1)
Console.Write("Element is not present in array");
else
Console.Write("Element is present at index "
+ result);
}
} PHP
<?php
// PHP program to find an element x in a
// sorted array using Exponential search.
// Returns position of first
// occurrence of x in array
function exponentialSearch($arr, $n, $x)
{
// If x is present at
// first location itself
if ($arr[0] == $x)
return 0;
// Find range for binary search
// by repeated doubling
$i = 1;
while ($i< $n and $arr[$i] <=$x)
$i = $i * 2;
// Call binary search
// for the found range.
return binarySearch($arr, $i / 2,
min($i, $n), $x);
}
// A recursive binary search
// function. It returns location
// of x in given array arr[l..r] is
// present, otherwise -1
function binarySearch($arr, $l,
$r, $x)
{
if ($r >= $l)
{
$mid = $l + ($r - $l)/2;
// If the element is
// present at the middle
// itself
if ($arr[$mid] == $x)
return $mid;
// If element is smaller
// than mid, then it
// can only be present
// n left subarray
if ($arr[$mid] > $x)
return binarySearch($arr, $l,
$mid - 1, $x);
// Else the element
// can only be present
// in right subarray
return binarySearch($arr, $mid + 1,
$r, $x);
}
// We reach here when
// element is not present
// in array
return -1;
}
// Driver code
$arr = array(2, 3, 4, 10, 40);
$n = count($arr);
$x = 10;
$result = exponentialSearch($arr, $n, $x);
if($result == -1)
echo "Element is not present in array";
else
echo "Element is present at index ",
$result;
?>
Kết quả
Element is present at index 33. Độ phức tạp
Độ phức tạp về thời gian: O (Log n)
Không gian phụ: Việc thực hiện Tìm kiếm nhị phân ở trên là đệ quy và yêu cầu không gian O (Log n). Với Tìm kiếm nhị phân lặp lại, chúng ta chỉ cần O (1) khoảng trắng.
4. Các ứng dụng của Tìm kiếm theo cấp số nhân(Exponential Search):
Tìm kiếm nhị phân theo hàm mũ đặc biệt hữu ích cho các tìm kiếm không giới hạn, trong đó kích thước của mảng là vô hạn. Vui lòng tham khảo Tìm kiếm nhị phân không giới hạn để biết ví dụ.
Nó hoạt động tốt hơn so với Tìm kiếm nhị phân đối với các mảng bị giới hạn và cũng như khi phần tử được tìm kiếm gần với phần tử đầu tiên hơn.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

