Chào ace, bài này chúng ta sẽ tìm hiểu về một trong các thuật toán sắp xếp được sử dụng nhiều trong lập trình và thực tế nhất đó là Merge Sort, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, ứng dụng của nó, code ví dụ, điểm mạnh, điểm yếu…) về Merge Sort thông qua các phần sau.
Nội dung chính
1. Giới thiệu
Giống như QuickSort, Merge Sort là một thuật toán Chia và Chinh phục. Nó chia mảng đầu vào thành hai nửa, gọi chính nó cho hai nửa và sau đó hợp nhất hai nửa đã sắp xếp. Hàm merge () được sử dụng để hợp nhất hai nửa. Hợp nhất (arr, l, m, r) là quá trình quan trọng giả định rằng arr [l..m] và arr [m + 1..r] được sắp xếp và hợp nhất hai mảng con đã sắp xếp thành một. Xem cách triển khai C sau để biết thêm chi tiết.
MergeSort (arr [], l, r)
Nếu r> l
1. Tìm điểm giữa để chia mảng thành hai nửa:
Ở giữa m = (l + r) / 2
2. Hợp nhất cuộc gọi Sắp xếp cho nửa đầu:
Gọi mergeSort(arr, l, m)
3. Hợp nhất cuộc gọi Sắp xếp cho nửa sau:
Gọi mergeSort(arr, m + 1, r)
4. Hợp nhất hai nửa được sắp xếp ở bước 2 và 3:
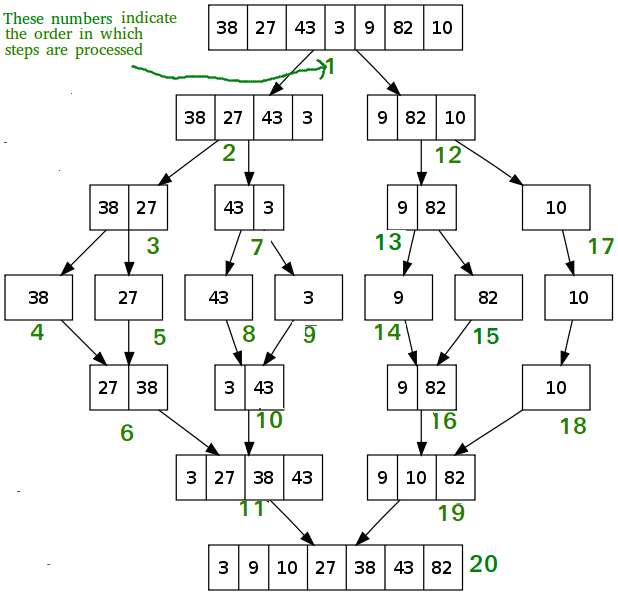
Gọi merge(arr, l, m, r)Sơ đồ sau đây từ wikipedia cho thấy quy trình sắp xếp hợp nhất hoàn chỉnh cho một mảng ví dụ {38, 27, 43, 3, 9, 82, 10}. Nếu chúng ta xem xét kỹ hơn sơ đồ, chúng ta có thể thấy rằng mảng được chia đệ quy làm hai nửa cho đến khi kích thước trở thành 1. Khi kích thước trở thành 1, các quá trình hợp nhất sẽ hoạt động và bắt đầu hợp nhất các mảng trở lại cho đến khi mảng hoàn chỉnh đã hợp nhất.
Hình ảnh minh hoạ
2. Code ví dụ trên nhiều ngôn ngữ
C++
// C++ program for Merge Sort
#include<iostream>
using namespace std;
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
// Create temp arrays
int L[n1], R[n2];
// Copy data to temp arrays L[] and R[]
for(int i = 0; i < n1; i++)
L[i] = arr[l + i];
for(int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
// Merge the temp arrays back into arr[l..r]
// Initial index of first subarray
int i = 0;
// Initial index of second subarray
int j = 0;
// Initial index of merged subarray
int k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of
// L[], if there are any
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// Copy the remaining elements of
// R[], if there are any
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// l is for left index and r is
// right index of the sub-array
// of arr to be sorted */
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// Same as (l+r)/2, but avoids
// overflow for large l and h
int m = l + (r - l) / 2;
// Sort first and second halves
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
for(int i = 0; i < size; i++)
cout << A[i] << " ";
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "\nSorted array is \n";
printArray(arr, arr_size);
return 0;
} C
/* C program for Merge Sort */
#include <stdio.h>
#include <stdlib.h>
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
/* create temp arrays */
int L[n1], R[n2];
/* Copy data to temp arrays L[] and R[] */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays back into arr[l..r]*/
i = 0; // Initial index of first subarray
j = 0; // Initial index of second subarray
k = l; // Initial index of merged subarray
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
/* Copy the remaining elements of L[], if there
are any */
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
/* Copy the remaining elements of R[], if there
are any */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
/* l is for left index and r is right index of the
sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int r)
{
if (l < r) {
// Same as (l+r)/2, but avoids overflow for
// large l and h
int m = l + (r - l) / 2;
// Sort first and second halves
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
/* UTILITY FUNCTIONS */
/* Function to print an array */
void printArray(int A[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", A[i]);
printf("\n");
}
/* Driver program to test above functions */
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
printf("Given array is \n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("\nSorted array is \n");
printArray(arr, arr_size);
return 0;
}
Java
/* Java program for Merge Sort */
class MergeSort {
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
// Find sizes of two subarrays to be merged
int n1 = m - l + 1;
int n2 = r - m;
/* Create temp arrays */
int L[] = new int[n1];
int R[] = new int[n2];
/*Copy data to temp arrays*/
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays */
// Initial indexes of first and second subarrays
int i = 0, j = 0;
// Initial index of merged subarry array
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
/* Copy remaining elements of L[] if any */
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
/* Copy remaining elements of R[] if any */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// Main function that sorts arr[l..r] using
// merge()
void sort(int arr[], int l, int r)
{
if (l < r) {
// Find the middle point
int m = (l + r) / 2;
// Sort first and second halves
sort(arr, l, m);
sort(arr, m + 1, r);
// Merge the sorted halves
merge(arr, l, m, r);
}
}
/* A utility function to print array of size n */
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver method
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
System.out.println("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.length - 1);
System.out.println("\nSorted array");
printArray(arr);
}
} Python3
# Python program for implementation of MergeSort
def mergeSort(arr):
if len(arr) >1:
mid = len(arr)//2 # Finding the mid of the array
L = arr[:mid] # Dividing the array elements
R = arr[mid:] # into 2 halves
mergeSort(L) # Sorting the first half
mergeSort(R) # Sorting the second half
i = j = k = 0
# Copy data to temp arrays L[] and R[]
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i+= 1
else:
arr[k] = R[j]
j+= 1
k+= 1
# Checking if any element was left
while i < len(L):
arr[k] = L[i]
i+= 1
k+= 1
while j < len(R):
arr[k] = R[j]
j+= 1
k+= 1
# Code to print the list
def printList(arr):
for i in range(len(arr)):
print(arr[i], end =" ")
print()
# driver code to test the above code
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
print ("Given array is", end ="\n")
printList(arr)
mergeSort(arr)
print("Sorted array is: ", end ="\n")
printList(arr) Kết quả
Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 133. Độ phức tạp
Độ phức tạp về thời gian: Sắp xếp các mảng trên các máy khác nhau. Merge Sort là một thuật toán đệ quy và độ phức tạp thời gian có thể được biểu thị như sau.
T (n) = 2T (n / 2) + θ (n)Sự lặp lại trên có thể được giải quyết bằng cách sử dụng phương pháp tree lặp lại hoặc phương pháp Master. Nó nằm trong trường hợp II của Phương pháp Master và nghiệm của sự tái diễn là θ (nLogn). Độ phức tạp thời gian của Sắp xếp hợp nhất(Merge Sort) là θ (nLogn) trong cả 3 trường hợp (xấu nhất, trung bình và tốt nhất) vì sắp xếp hợp nhất luôn chia mảng thành hai nửa và mất thời gian tuyến tính để hợp nhất hai nửa.
Không gian phụ trợ: O (n)
Mô hình thuật toán: Chia và Chinh phục
Ổn định: Có
4. Ứng dụng
- Merge Sort rất hữu ích để sắp xếp các danh sách được liên kết trong thời gian O (nLogn). Trong trường hợp danh sách được liên kết, trường hợp này khác nhau chủ yếu do sự khác biệt trong phân bổ bộ nhớ của mảng và danh sách được liên kết. Không giống như mảng, các nút danh sách liên kết có thể không liền kề trong bộ nhớ. Không giống như một mảng, trong danh sách liên kết, chúng ta có thể chèn các mục vào giữa trong O (1) không gian thừa và O (1) thời gian. Do đó hoạt động hợp nhất của sắp xếp hợp nhất có thể được thực hiện mà không có thêm dung lượng cho danh sách được liên kết. Trong mảng, chúng ta có thể thực hiện truy cập ngẫu nhiên khi các phần tử nằm kề nhau trong bộ nhớ. Giả sử chúng ta có một mảng A số nguyên (4 byte) và đặt địa chỉ của A [0] là x thì để truy cập A [i], chúng ta có thể truy cập trực tiếp vào bộ nhớ tại (x + i * 4). Không giống như mảng, chúng ta không thể thực hiện truy cập ngẫu nhiên trong danh sách liên kết. Sắp xếp nhanh yêu cầu rất nhiều loại truy cập. Trong danh sách liên kết để truy cập chỉ mục thứ i, chúng ta phải di chuyển từng nút từ đầu đến nút thứ i vì chúng ta không có khối bộ nhớ liên tục. Do đó, chi phí tăng đối với nhanh chóng. Sắp xếp hợp nhất truy cập dữ liệu một cách tuần tự và nhu cầu truy cập ngẫu nhiên thấp.
- Vấn đề đảo ngược số lượng
- Được sử dụng trong sắp xếp bên ngoài
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

