Trong bài này chúng ta sẽ tiếp cận với cơ chế được dùng nhiều trong các thuật toán đó là cách phân chia để trị(Divide and Conquer) hay chia để chinh phục, nhắm giúp thuật toán nhanh và hiệu quả hơn.
Nội dung chính
1. Giới thiệu
Trong cách tiếp cận phân chia và chinh phục(chia để trị), bài toán được chia thành các bài toán con nhỏ hơn và sau đó mỗi bài toán được giải quyết độc lập. Khi chúng ta tiếp tục chia các bài toán con thành các bài toán con nhỏ hơn, cuối cùng chúng ta có thể đạt đến một giai đoạn mà không thể phân chia được nữa. Những vấn đề con nhỏ nhất có thể có “nguyên tử” (phân số) được giải quyết. Lời giải của tất cả các bài toán con cuối cùng được hợp nhất để có được lời giải của một bài toán ban đầu.
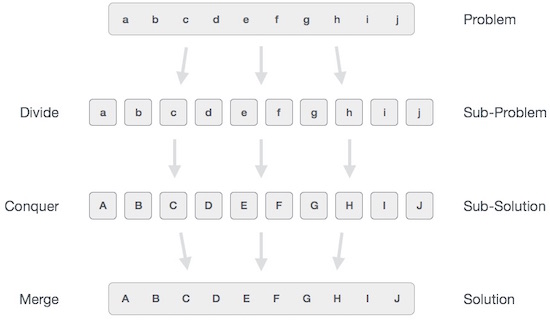
Nhìn chung, chúng ta có thể hiểu cách tiếp cận chia để trị trong quy trình ba bước sau:
2. Phân chia hoặc ngắt(Divide/Break)
Bước này liên quan đến việc chia nhỏ vấn đề thành các vấn đề nhỏ hơn. Các vấn đề phụ nên đại diện cho một phần của vấn đề ban đầu. Bước này thường sử dụng một cách tiếp cận đệ quy để chia bài toán cho đến khi không có bài toán con nào có thể chia được nữa. Ở giai đoạn này, các vấn đề phụ trở thành nguyên tử về bản chất nhưng vẫn thể hiện một phần nào đó của vấn đề thực tế.
3. Chinh phục / Giải quyết(Conquer/Solve)
Bước này nhận được rất nhiều vấn đề nhỏ hơn cần giải quyết. Nói chung, ở cấp độ này, các vấn đề được coi là ‘tự giải quyết’.
4. Hợp nhất / Kết hợp(Merge/Combine)
Khi các bài toán con nhỏ hơn được giải quyết, giai đoạn này kết hợp chúng một cách đệ quy cho đến khi chúng tạo thành một giải pháp của bài toán ban đầu. Cách tiếp cận thuật toán này bằng hoạt động đệ quy các bước chinh phục & hợp nhất chúng gần nhau đến mức chúng xuất hiện thành một.
Ví dụ
Các thuật toán máy tính sau đây dựa trên cách tiếp cận lập trình chia để trị:
- Hợp nhất Sắp xếp(Merge Sort)
- Sắp xếp nhanh chóng(Quick Sort)
- Tìm kiếm nhị phân(Binary Search)
- Phép nhân ma trận của Strassen(Strassen’s Matrix Multiplication)
- Cặp gần nhất (điểm)(Closest pair (points))
Có nhiều cách khác nhau có sẵn để giải quyết bất kỳ vấn đề máy tính nào, nhưng những cách được đề cập là một ví dụ điển hình về phương pháp chia và chinh phục.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
 hay chia để chinh phục, nhắm giúp thuật toán nhanh và hiệu quả hơn.){kind=link}