Chào ace, bài này chúng ta sẽ tìm hiểu về Merge Sort cho danh sách liên kết đơn – Singly Linked List và danh sách liên kết kép – Doubly Linked List trong series tự học về cấu trúc dữ liệu(CTDL) và giải thuật, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, độ phức tạp, ứng dụng của nó, code ví dụ…) về nó thông qua các phần sau.
Nội dung chính
1. MergeSort dành cho Singly Linked List
Merge sort thường được ưu tiên sử dụng để sắp xếp danh sách liên kết – linked list nói chung (cả danh sách liên kết đơn và kép). Vấn đề hiệu suất truy cập ngẫu nhiên chậm của linked list làm cho một số thuật toán khác (chẳng hạn như QuickSort) hoạt động kém hiệu quả, và những thuật toán khác (chẳng hạn như HeapSort) hoàn toàn không thể cài đặt được.
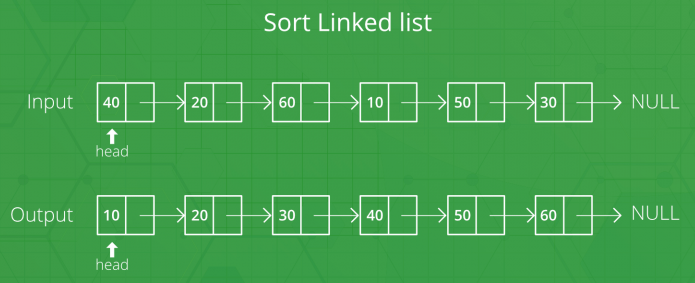
Lấy con trỏ head là node đầu tiên của linked list sẽ được sắp xếp, và con trỏ headRef trỏ tới node head. Lưu ý rằng chúng ta cần có được một tham chiếu (reference) đến node head trong hàm MergeSort() bởi vì trong đoạn code ví dụ cài đặt MergeSort cho linked list bên dưới đây, chúng ta sẽ thay đổi các liên kết con trỏ next của các nodes để sắp xếp linked list (chứ không phải tiến hành sắp xếp dựa trên việc thay đổi các phần dữ liệu của các nodes), vì vậy phải thay đổi node head (tức là làm cho một node khác trở thành node head mới) nếu phần dữ liệu của node head ban đầu không phải là giá trị nhỏ nhất trong linked list.
* Mô tả thuật toán MergeSort dành cho Singly Linked List
MergeSort(headRef)
1. Nếu node head/con trỏ head là NULL, hoặc là chỉ có duy nhất một phần tử bên trong Linked List, vậy thì ta sẽ return luôn.
2. Nếu không rơi vào trường hợp ở bước 1, ta sẽ chia đôi linked list thành 2 nửa.
FrontBackSplit(head, &a, &b); /* a và b chính là 2 nửa của linked list */
3. Tiến hành sắp xếp 2 nửa là nửa a và nửa b của linked list.
MergeSort(a);
MergeSort(b);
4. Hợp nhất nửa a đã được sắp xếp và nửa b đã được sắp xếp của linked list ở bước 3 vào với nhau (bằng cách sử dụng hàm SortedMerge()) và cập nhật lại con trỏ head bằng cách sử udngj con trỏ headRef.
*headRef = SortedMerge(a, b);
2. MergeSort dành cho Doubly Linked List
Trong phần này chúng ta sẽ tìm hiểu về cách để viết một hàm có chức năng sắp xếp danh sách liên kết kép – doubly linked list theo thứ tự tăng dần bằng cách sử dụng merge sort.
Ví dụ, ta có danh sách liên kết ban đầu ở dạng:
Sau khi sắp xếp, danh sách liên kết kép trên sẽ trở thành 2 -> 4 -> 8 -> 10
Cách cài đặt thuật toán MergeSort cho Doubly Linked List cũng tương tự như áp dụng cho Singly Linked List (đã được mô tả ở phần trước), chỉ khác ở 1 điểm quan trọng đó là đối với Doubly Linked List, chúng ta sẽ phải chỉnh sửa các con trỏ previous khi hơp hai danh sách lại với nhau.
Dưới đây là các đoạn code ví dụ cài đặt thuật toán MergeSort cho danh sách liên kết kép – Doubly Linked List.
CÁC ĐOẠN CODE CÀI ĐẶT THUẬT TOÁN ĐƯỢC VIẾT BẰNG C++ C JAVA PYTHON C#
C
// C program for merge sort on doubly linked list
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node *next, *prev;
};
struct Node *split(struct Node *head);
// Function to merge two linked lists
struct Node *merge(struct Node *first, struct Node *second)
{
// If first linked list is empty
if (!first)
return second;
// If second linked list is empty
if (!second)
return first;
// Pick the smaller value
if (first->data < second->data)
{
first->next = merge(first->next,second);
first->next->prev = first;
first->prev = NULL;
return first;
}
else
{
second->next = merge(first,second->next);
second->next->prev = second;
second->prev = NULL;
return second;
}
}
// Function to do merge sort
struct Node *mergeSort(struct Node *head)
{
if (!head || !head->next)
return head;
struct Node *second = split(head);
// Recur for left and right halves
head = mergeSort(head);
second = mergeSort(second);
// Merge the two sorted halves
return merge(head,second);
}
// A utility function to insert a new node at the
// beginning of doubly linked list
void insert(struct Node **head, int data)
{
struct Node *temp =
(struct Node *)malloc(sizeof(struct Node));
temp->data = data;
temp->next = temp->prev = NULL;
if (!(*head))
(*head) = temp;
else
{
temp->next = *head;
(*head)->prev = temp;
(*head) = temp;
}
}
// A utility function to print a doubly linked list in
// both forward and backward directions
void print(struct Node *head)
{
struct Node *temp = head;
printf("Forward Traversal using next poitner\n");
while (head)
{
printf("%d ",head->data);
temp = head;
head = head->next;
}
printf("\nBackward Traversal using prev pointer\n");
while (temp)
{
printf("%d ", temp->data);
temp = temp->prev;
}
}
// Utility function to swap two integers
void swap(int *A, int *B)
{
int temp = *A;
*A = *B;
*B = temp;
}
// Split a doubly linked list (DLL) into 2 DLLs of
// half sizes
struct Node *split(struct Node *head)
{
struct Node *fast = head,*slow = head;
while (fast->next && fast->next->next)
{
fast = fast->next->next;
slow = slow->next;
}
struct Node *temp = slow->next;
slow->next = NULL;
return temp;
}
// Driver program
int main(void)
{
struct Node *head = NULL;
insert(&head,5);
insert(&head,20);
insert(&head,4);
insert(&head,3);
insert(&head,30);
insert(&head,10);
head = mergeSort(head);
printf("\n\nLinked List after sorting\n");
print(head);
return 0;
}
C++
// C++ program for merge sort on doubly linked list
#include <bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node *next, *prev;
};
Node *split(Node *head);
// Function to merge two linked lists
Node *merge(Node *first, Node *second)
{
// If first linked list is empty
if (!first)
return second;
// If second linked list is empty
if (!second)
return first;
// Pick the smaller value
if (first->data < second->data)
{
first->next = merge(first->next,second);
first->next->prev = first;
first->prev = NULL;
return first;
}
else
{
second->next = merge(first,second->next);
second->next->prev = second;
second->prev = NULL;
return second;
}
}
// Function to do merge sort
Node *mergeSort(Node *head)
{
if (!head || !head->next)
return head;
Node *second = split(head);
// Recur for left and right halves
head = mergeSort(head);
second = mergeSort(second);
// Merge the two sorted halves
return merge(head,second);
}
// A utility function to insert a new node at the
// beginning of doubly linked list
void insert(Node **head, int data)
{
Node *temp = new Node();
temp->data = data;
temp->next = temp->prev = NULL;
if (!(*head))
(*head) = temp;
else
{
temp->next = *head;
(*head)->prev = temp;
(*head) = temp;
}
}
// A utility function to print a doubly linked list in
// both forward and backward directions
void print(Node *head)
{
Node *temp = head;
cout<<"Forward Traversal using next poitner\n";
while (head)
{
cout << head->data << " ";
temp = head;
head = head->next;
}
cout << "\nBackward Traversal using prev pointer\n";
while (temp)
{
cout << temp->data << " ";
temp = temp->prev;
}
}
// Utility function to swap two integers
void swap(int *A, int *B)
{
int temp = *A;
*A = *B;
*B = temp;
}
// Split a doubly linked list (DLL) into 2 DLLs of
// half sizes
Node *split(Node *head)
{
Node *fast = head,*slow = head;
while (fast->next && fast->next->next)
{
fast = fast->next->next;
slow = slow->next;
}
Node *temp = slow->next;
slow->next = NULL;
return temp;
}
// Driver program
int main(void)
{
Node *head = NULL;
insert(&head, 5);
insert(&head, 20);
insert(&head, 4);
insert(&head, 3);
insert(&head, 30);
insert(&head, 10);
head = mergeSort(head);
cout << "Linked List after sorting\n";
print(head);
return 0;
} Java
// Java program to implement merge sort in singly linked list
// Linked List Class
class LinkedList {
static Node head; // head of list
/* Node Class */
static class Node {
int data;
Node next, prev;
// Constructor to create a new node
Node(int d) {
data = d;
next = prev = null;
}
}
void print(Node node) {
Node temp = node;
System.out.println("Forward Traversal using next pointer");
while (node != null) {
System.out.print(node.data + " ");
temp = node;
node = node.next;
}
System.out.println("\nBackward Traversal using prev pointer");
while (temp != null) {
System.out.print(temp.data + " ");
temp = temp.prev;
}
}
// Split a doubly linked list (DLL) into 2 DLLs of
// half sizes
Node split(Node head) {
Node fast = head, slow = head;
while (fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
Node temp = slow.next;
slow.next = null;
return temp;
}
Node mergeSort(Node node) {
if (node == null || node.next == null) {
return node;
}
Node second = split(node);
// Recur for left and right halves
node = mergeSort(node);
second = mergeSort(second);
// Merge the two sorted halves
return merge(node, second);
}
// Function to merge two linked lists
Node merge(Node first, Node second) {
// If first linked list is empty
if (first == null) {
return second;
}
// If second linked list is empty
if (second == null) {
return first;
}
// Pick the smaller value
if (first.data < second.data) {
first.next = merge(first.next, second);
first.next.prev = first;
first.prev = null;
return first;
} else {
second.next = merge(first, second.next);
second.next.prev = second;
second.prev = null;
return second;
}
}
// Driver program to test above functions
public static void main(String[] args) {
LinkedList list = new LinkedList();
list.head = new Node(10);
list.head.next = new Node(30);
list.head.next.next = new Node(3);
list.head.next.next.next = new Node(4);
list.head.next.next.next.next = new Node(20);
list.head.next.next.next.next.next = new Node(5);
Node node = null;
node = list.mergeSort(head);
System.out.println("Linked list after sorting :");
list.print(node);
}
} Python
# Program for merge sort on doubly linked list
# A node of the doublly linked list
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
class DoublyLinkedList:
# Constructor for empty Doubly Linked List
def __init__(self):
self.head = None
# Function to merge two linked list
def merge(self, first, second):
# If first linked list is empty
if first is None:
return second
# If secon linked list is empty
if second is None:
return first
# Pick the smaller value
if first.data < second.data:
first.next = self.merge(first.next, second)
first.next.prev = first
first.prev = None
return first
else:
second.next = self.merge(first, second.next)
second.next.prev = second
second.prev = None
return second
# Function to do merge sort
def mergeSort(self, tempHead):
if tempHead is None:
return tempHead
if tempHead.next is None:
return tempHead
second = self.split(tempHead)
# Recur for left and righ halves
tempHead = self.mergeSort(tempHead)
second = self.mergeSort(second)
# Merge the two sorted halves
return self.merge(tempHead, second)
# Split the doubly linked list (DLL) into two DLLs
# of half sizes
def split(self, tempHead):
fast = slow = tempHead
while(True):
if fast.next is None:
break
if fast.next.next is None:
break
fast = fast.next.next
slow = slow.next
temp = slow.next
slow.next = None
return temp
# Given a reference to the head of a list and an
# integer,inserts a new node on the front of list
def push(self, new_data):
# 1. Allocates node
# 2. Put the data in it
new_node = Node(new_data)
# 3. Make next of new node as head and
# previous as None (already None)
new_node.next = self.head
# 4. change prev of head node to new_node
if self.head is not None:
self.head.prev = new_node
# 5. move the head to point to the new node
self.head = new_node
def printList(self, node):
temp = node
print "Forward Traversal using next poitner"
while(node is not None):
print node.data,
temp = node
node = node.next
print "\nBackward Traversal using prev pointer"
while(temp):
print temp.data,
temp = temp.prev
# Driver program to test the above functions
dll = DoublyLinkedList()
dll.push(5)
dll.push(20);
dll.push(4);
dll.push(3);
dll.push(30)
dll.push(10);
dll.head = dll.mergeSort(dll.head)
print "Linked List after sorting"
dll.printList(dll.head)
C#
// C# program to implement merge
// sort in singly linked list
using System;
// Linked List Class
public class LinkedList
{
Node head; // head of list
/* Node Class */
class Node
{
public int data;
public Node next, prev;
// Constructor to create a new node
public Node(int d)
{
data = d;
next = prev = null;
}
}
void print(Node node)
{
Node temp = node;
Console.WriteLine("Forward Traversal" +
"using next pointer");
while (node != null)
{
Console.Write(node.data + " ");
temp = node;
node = node.next;
}
Console.WriteLine("\nBackward Traversal" +
"using prev pointer");
while (temp != null)
{
Console.Write(temp.data + " ");
temp = temp.prev;
}
}
// Split a doubly linked list (DLL)
// into 2 DLLs of half sizes
Node split(Node head)
{
Node fast = head, slow = head;
while (fast.next != null &&
fast.next.next != null)
{
fast = fast.next.next;
slow = slow.next;
}
Node temp = slow.next;
slow.next = null;
return temp;
}
Node mergeSort(Node node)
{
if (node == null || node.next == null)
{
return node;
}
Node second = split(node);
// Recur for left and right halves
node = mergeSort(node);
second = mergeSort(second);
// Merge the two sorted halves
return merge(node, second);
}
// Function to merge two linked lists
Node merge(Node first, Node second)
{
// If first linked list is empty
if (first == null) {
return second;
}
// If second linked list is empty
if (second == null)
{
return first;
}
// Pick the smaller value
if (first.data < second.data)
{
first.next = merge(first.next, second);
first.next.prev = first;
first.prev = null;
return first;
}
else
{
second.next = merge(first, second.next);
second.next.prev = second;
second.prev = null;
return second;
}
}
// Driver code
public static void Main(String[] args)
{
LinkedList list = new LinkedList();
list.head = new Node(10);
list.head.next = new Node(30);
list.head.next.next = new Node(3);
list.head.next.next.next = new Node(4);
list.head.next.next.next.next = new Node(20);
list.head.next.next.next.next.next = new Node(5);
Node node = null;
node = list.mergeSort(list.head);
Console.WriteLine("Linked list after sorting :");
list.print(node);
}
} Kết quả in ra là:
Linked List after sorting
Forward Traversal using next pointer
3 4 5 10 20 30
Backward Traversal using prev pointer
30 20 10 5 4 3Độ phức tạp về thời gian: Độ phức tạp về thời gian của các đoạn code cài đặt thuật toán MergeSort dành cho Doubly Linked List ở trên thì giống với độ phức tạp về thời gian khi cài đặt MergeSort cho mảng một chiều, đều phải mất O(nLogn) thời gian.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
