Trang chủ Thế giới ngôn ngữ lập trình - Programming Languages Tự học Javascript Đệ quy và ngăn xếp(stack), Linked list trong Javascript

[Tự học Javascript] Đệ quy và ngăn xếp(stack), Linked list trong Javascript

Recursion and stack in Javascript

Bởi

David Xuân

24 Tháng Năm, 2020

1446

🔥CHỌN LỌC TOP NHỮNG KHOÁ HỌC LẬP TRÌNH ONLINE NHIỀU NGƯỜI THEO HOC TẠI ĐÂY🔥

Hãy quay trở lại các hàm và nghiên cứu chúng sâu hơn.

Chủ đề đầu tiên của chúng ta sẽ là đệ quy(Recursion).

Nếu bạn chưa quen với lập trình, thì có lẽ bạn có thể bỏ qua chương này.

Đệ quy(Recursion) là một mẫu lập trình rất hữu ích trong các tình huống khi một tác vụ có thể được phân chia tự nhiên thành nhiều nhiệm vụ cùng loại, nhưng đơn giản hơn. Hoặc khi một tác vụ có thể được đơn giản hóa thành một hành động dễ dàng cộng với một biến thể đơn giản hơn của cùng một tác vụ. Hoặc, như chúng ta sẽ thấy sớm, để đối phó với các cấu trúc dữ liệu nhất định.

Khi một hàm giải quyết một nhiệm vụ, trong quá trình nó có thể gọi nhiều hàm khác. Một trường hợp một phần của điều này là khi một hàm gọi lại chính nó . Đó gọi là đệ quy(Recursion).

Nội dung chính

1. Hai cách nghĩ

Đối với một cái gì đó đơn giản để bắt đầu – hãy viết một hàm pow(x, n)tăng x lên với n. Nói cách khác, nhân x lên với nlần.

pow(2, 2) = 4
pow(2, 3) = 8
pow(2, 4) = 16

Có hai cách để thực hiện nó.

Suy nghĩ lặp lại: vòng lặp for:

function pow(x, n) {   
let result = 1;   // multiply result by x n times in the loop   
for (let i = 0; i < n; i++) {     
  result *= x;  
 }   
return result; 
}
alert( pow(2, 3) ); // 8

Tư duy đệ quy: đơn giản hóa nhiệm vụ và tự gọi:

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

alert( pow(2, 3) ); // 8

Xin lưu ý cách biến thể đệ quy khác nhau về cơ bản.

Khi pow(x, n)được gọi, thực thi chia thành hai nhánh:

              if n==1  = x
             /
pow(x, n) =
             \
              else     = x * pow(x, n - 1)

Nếu n == 1, thì mọi thứ đều bình thường. Nó được gọi là cơ sở của đệ quy, bởi vì nó ngay lập tức tạo ra kết quả rõ ràng: pow(x, 1)bằng x.
Nếu không, chúng ta có thể đại diện pow(x, n)như x * pow(x, n - 1). Trong toán học, người ta sẽ viết vậy. Đây được gọi là bước đệ quy : chúng ta chuyển đổi nhiệm vụ thành một hành động đơn giản hơn (nhân với) và một lệnh gọi đơn giản hơn của cùng một nhiệm vụ ( với mức thấp hơn ). Các bước tiếp theo đơn giản hóa nó hơn nữa và cho đến khi đạt được .xⁿ = x * x^n-1xpownn1

Chúng ta cũng có thể nói rằng pow đệ quy gọi chính nó cho đến khi n == 1.

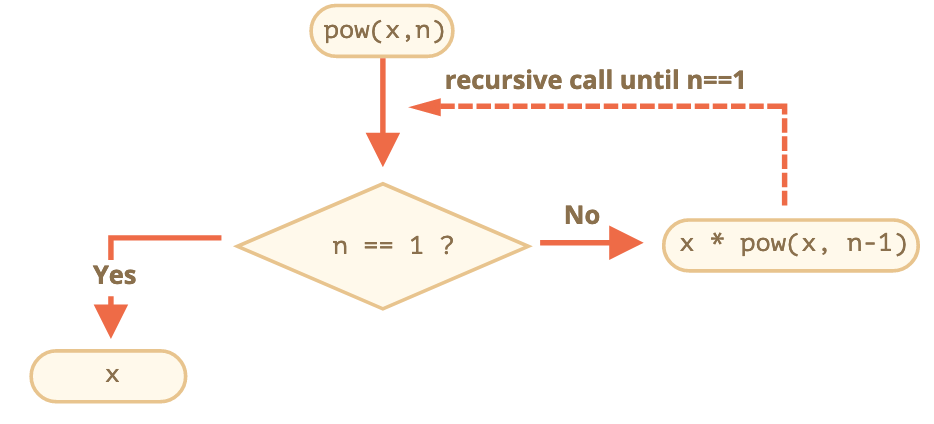
Ví dụ, để tính toán pow(2, 4)biến thể đệ quy thực hiện các bước sau:

pow(2, 4) = 2 * pow(2, 3)
pow(2, 3) = 2 * pow(2, 2)
pow(2, 2) = 2 * pow(2, 1)
pow(2, 1) = 2

Vì vậy, đệ quy giảm một cuộc gọi hàm đến một hàm khác thay vì gọi nó, và sau đó – thậm chí còn đơn giản hơn, và cho đến khi kết quả trở được trả về.

Đệ quy thường ngắn hơn

Một giải pháp đệ quy thường ngắn hơn một giải pháp lặp lại.

Ở đây chúng ta có thể viết lại tương tự bằng cách sử dụng toán tử có điều kiện ?thay vì ifđể pow(x, n)ngắn gọn hơn và vẫn rất dễ đọc:

function pow(x, n) {
  return (n == 1) ? x : (x * pow(x, n - 1));
}

Số lượng tối đa của các cuộc gọi lồng nhau (bao gồm cả cuộc gọi đầu tiên) được gọi là độ sâu đệ quy . Trong trường hợp của chúng ta, nó sẽ chính xác n.

Độ sâu đệ quy tối đa bị giới hạn bởi công cụ JavaScript. Chúng ta có thể dựa vào nó là 10000, một số động cơ cho phép nhiều hơn, nhưng 100000 có lẽ là vượt quá giới hạn cho phần lớn trong số họ. Có những tối ưu hóa tự động giúp giảm bớt điều này ( gọi là tối ưu hóa), nhưng chúng chưa được hỗ trợ ở mọi nơi và chỉ hoạt động trong những trường hợp đơn giản.

Điều đó giới hạn việc áp dụng đệ quy, nhưng nó vẫn còn rất rộng. Có nhiều nhiệm vụ trong đó cách suy nghĩ đệ quy cho mã đơn giản hơn, dễ bảo trì hơn.

2. Bối cảnh thực hiện và ngăn xếp

Bây giờ hãy xem xét cách các cuộc gọi đệ quy hoạt động. Cho rằng chúng ta sẽ xem xét các hàm.

Thông tin về quá trình thực thi của một hàm đang chạy được lưu trữ trong bối cảnh thực hiện của nó .

Các bối cảnh thực hiện là một cấu trúc dữ liệu nội bộ có chứa thông tin chi tiết về việc thực hiện một hàm: nơi kiểm soát dòng chảy hiện nay, các biến hiện tại, giá trị của this(chúng ta không sử dụng nó ở đây) và vài chi tiết nội bộ khác.

Một cuộc gọi hàm có chính xác một bối cảnh thực hiện liên quan đến nó.

Khi một hàm thực hiện một cuộc gọi lồng nhau, điều sau đây xảy ra:

Hàm hiện tại bị tạm dừng.
Bối cảnh thực hiện liên quan đến nó được ghi nhớ trong một cấu trúc dữ liệu đặc biệt gọi là ngăn xếp bối cảnh thực thi .
Cuộc gọi lồng nhau thực thi.
Sau khi kết thúc, bối cảnh thực thi cũ được lấy từ ngăn xếp và hàm bên ngoài được nối lại từ nơi nó dừng lại.

Chúng ta hãy xem những gì xảy ra trong pow(2, 3).

2.1. pow (2, 3)

Khi bắt đầu cuộc gọi pow(2, 3), bối cảnh thực hiện sẽ lưu trữ các biến : x = 2, n = 3, luồng thực thi nằm ở dòng 1của hàm.

Chúng ta có thể phác họa nó như sau:

Bối cảnh: {x: 2, n: 3, tại dòng 1} gọi pow (2, 3)

Đó là khi hàm bắt đầu thực thi. Điều kiện n == 1là sai, vì vậy dòng chảy tiếp tục vào nhánh thứ hai của if:

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

alert( pow(2, 3) );

Các biến giống nhau, nhưng dòng thay đổi, vì vậy bối cảnh bây giờ là:

Bối cảnh: {x: 2, n: 3, tại dòng 5} gọi pow (2, 3)

Để tính toán x * pow(x, n - 1), chúng ta cần tạo một tập hợp con powvới các đối số mới pow(2, 2).

2.2. pow (2, 2)

Để thực hiện một cuộc gọi lồng nhau, JavaScript ghi nhớ bối cảnh thực hiện hiện tại trong ngăn xếp bối cảnh thực hiện .

Ở đây chúng ta gọi hàm tương tự pow, nhưng nó hoàn toàn không thành vấn đề. Quá trình này giống nhau cho tất cả các hàm:

Bối cảnh hiện tại là Hồi nhớ trên đỉnh ngăn xếp.
Bối cảnh mới được tạo ra được gọi là lệnh gọi con(subcall).
Khi subcall kết thúc – bối cảnh trước đó được bật ra khỏi ngăn xếp và quá trình thực thi của nó tiếp tục.

Đây là ngăn xếp bối cảnh khi chúng ta nhập subcall pow(2, 2):

Bối cảnh: {x: 2, n: 2, tại dòng 1} pow (2, 2)
Bối cảnh: {x: 2, n: 3, tại dòng 5} pow (2, 3)

Bối cảnh thực hiện hiện tại mới ở trên cùng (và đậm) và các bối cảnh được nhớ trước đó ở bên dưới.

Khi chúng ta hoàn thành subcall – thật dễ dàng để tiếp tục bối cảnh trước đó, bởi vì nó giữ cả hai biến và vị trí chính xác của mã nơi nó dừng lại.

Xin lưu ý:

Ở đây trong bức ảnh, chúng ta sử dụng từ dòng, vì dụ của chúng ta chỉ có một dòng con trong dòng, nhưng nói chung, một dòng code có thể chứa nhiều chuỗi con, như pow(…) + pow(…) + somethingElse(…).

Vì vậy, sẽ chính xác hơn khi nói rằng vụ hành quyết lại tiếp tục ngay lập tức sau khi có subcall.

2.3. pow (2, 1)

Quá trình lặp lại: một subcall mới được thực hiện tại dòng 5, bây giờ với các đối số x=2, n=1.

Một bối cảnh thực hiện mới được tạo ra, bối cảnh trước đó được đẩy lên trên cùng của ngăn xếp:

Bối cảnh: {x: 2, n: 1, tại dòng 1} pow (2, 1)
Bối cảnh: {x: 2, n: 2, tại dòng 5} pow (2, 2)
Bối cảnh: {x: 2, n: 3, tại dòng 5} pow (2, 3)

Hiện có 2 bối cảnh cũ và 1 bối cảnh hiện đang chạy pow(2, 1).

2.4. Lối thoát

Trong quá trình thực hiện pow(2, 1), không giống như trước đây, điều kiện n == 1là trung thực, vì vậy nhánh đầu tiên của ifcông trình:

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

Không có nhiều cuộc gọi lồng nhau, vì vậy hàm kết thúc, trả lại 2.

Khi hàm kết thúc, bối cảnh thực thi của nó không còn cần thiết nữa, vì vậy nó bị xóa khỏi bộ nhớ. Cái trước được khôi phục khỏi đầu ngăn xếp:

Bối cảnh: {x: 2, n: 2, tại dòng 5} pow (2, 2)
Bối cảnh: {x: 2, n: 3, tại dòng 5} pow (2, 3)

Việc thực hiện pow(2, 2)được nối lại. Nó có kết quả của subcall pow(2, 1), vì vậy nó cũng có thể hoàn thành việc đánh giá x * pow(x, n - 1), trả lại 4.

Sau đó, bối cảnh trước đó được khôi phục:

Bối cảnh: {x: 2, n: 3, tại dòng 5} pow (2, 3)

Khi nó kết thúc, chúng ta có một kết quả pow(2, 3) = 8.

Độ sâu đệ quy trong trường hợp này là: 3 .

Như chúng ta có thể thấy từ các minh họa ở trên, độ sâu đệ quy bằng với số lượng bối cảnh tối đa trong ngăn xếp.

Lưu ý các yêu cầu bộ nhớ. Bối cảnh mất bộ nhớ. Trong trường hợp của chúng ta, việc nâng cao sức mạnh nthực sự đòi hỏi bộ nhớ cho ncác bối cảnh, cho tất cả các giá trị thấp hơn của n.

Một thuật toán dựa trên vòng lặp là tiết kiệm bộ nhớ hơn:

function pow(x, n) {
  let result = 1;

  for (let i = 0; i < n; i++) {
    result *= x;
  }

  return result;
}

Lặp lại powsử dụng một thay đổi bối cảnh duy nhất ivà resulttrong quá trình. Yêu cầu bộ nhớ của nó là nhỏ, cố định và không phụ thuộc vào n.

Bất kỳ đệ quy có thể được viết lại như một vòng lặp. Các biến thể vòng lặp thường có thể được thực hiện hiệu quả hơn.

Tuy nhiên, đôi khi việc viết lại thì không tầm thường, đặc biệt là khi hàm sử dụng các tiểu đệ quy khác nhau tùy thuộc vào điều kiện và hợp nhất kết quả của chúng hoặc khi phân nhánh phức tạp hơn. Và việc tối ưu hóa có thể là không cần thiết và hoàn toàn không xứng đáng với những nỗ lực.

Đệ quy có thể cung cấp một code ngắn hơn, dễ hiểu và hỗ trợ hơn. Tối ưu hóa không bắt buộc ở mọi nơi, chủ yếu chúng ta cần một code tốt, đó là lý do tại sao nó được sử dụng.

3. Chuyển tiếp đệ quy

Một ứng dụng tuyệt vời khác của đệ quy là một giao thức đệ quy.

Hãy tưởng tượng, chúng ta có một công ty. Cấu trúc nhân viên có thể được trình bày như một đối tượng:

let company = {
  sales: [{
    name: 'John',
    salary: 1000
  }, {
    name: 'Alice',
    salary: 1600
  }],

  development: {
    sites: [{
      name: 'Peter',
      salary: 2000
    }, {
      name: 'Alex',
      salary: 1800
    }],

    internals: [{
      name: 'Jack',
      salary: 1300
    }]
  }
};

Nói cách khác, một công ty có các phòng ban.

Một bộ phận có thể có một loạt các nhân viên. Chẳng hạn, salesbộ phận có 2 nhân viên: John và Alice.
Hoặc một bộ phận có thể chia thành các bộ phận, như developmentcó hai chi nhánh: sitesvà internals. Mỗi người trong số họ có nhân viên riêng của họ.
Cũng có thể là khi một phân khu phát triển, nó sẽ chia thành các phân khu (hoặc các nhóm). Ví dụ, sitesbộ phận trong tương lai có thể được chia thành các nhóm cho siteAvà siteB. Và họ, có khả năng, có thể chia nhiều hơn. Đó không phải là trên hình ảnh, chỉ là một cái gì đó để có trong tâm trí.

Bây giờ hãy nói rằng chúng ta muốn một hàm để có được tổng số tiền lương. Làm thế nào chúng ta có thể làm điều đó?

Một cách tiếp cận lặp đi lặp lại là không dễ dàng, bởi vì cấu trúc không đơn giản. Ý tưởng đầu tiên có thể là tạo một forvòng lặp companyvới các phân nhóm lồng nhau trên các phòng ban cấp 1. Nhưng sau đó, chúng ta cần nhiều phân nhóm lồng nhau hơn để lặp lại các nhân viên trong các phòng ban cấp 2 như Tập sitesvà sau đó một phân nhóm khác trong các phân khu cho các phòng ban cấp 3 có thể xuất hiện trong tương lai? Nếu chúng ta đặt 3-4 subloop lồng nhau trong mã để duyệt qua một đối tượng, nó sẽ trở nên khá xấu xí.

Hãy thử đệ quy.

Như chúng ta có thể thấy, khi hàm của chúng ta có một bộ phận để tổng hợp, có hai trường hợp có thể xảy ra:

Hoặc đó là một bộ phận đơn giản với một loạt người – sau đó chúng ta có thể tính tổng lương theo một vòng lặp đơn giản.
Hoặc đó là một đối tượng có các Nphân mục – sau đó chúng ta có thể thực hiện Ncác cuộc gọi đệ quy để lấy tổng cho từng phân mục và kết hợp các kết quả.

Trường hợp thứ nhất là cơ sở của đệ quy, trường hợp tầm thường, khi chúng ta nhận được một mảng.

Trường hợp thứ 2 khi chúng ta nhận được một đối tượng là bước đệ quy. Một nhiệm vụ phức tạp được chia thành các nhiệm vụ cho các phòng ban nhỏ hơn. Họ có thể lần lượt tách ra một lần nữa, nhưng sớm hay muộn sự phân chia sẽ kết thúc ở (1).

Thuật toán có thể dễ đọc hơn từ code:

/*
Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
@author cafedevn
Contact: cafedevn@gmail.com
Fanpage: https://www.facebook.com/cafedevn
Instagram: https://instagram.com/cafedevn
Twitter: https://twitter.com/CafedeVn
Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
*/

let company = { // the same object, compressed for brevity
  sales: [{name: 'John', salary: 1000}, {name: 'Alice', salary: 1600 }],
  development: {
    sites: [{name: 'Peter', salary: 2000}, {name: 'Alex', salary: 1800 }],
    internals: [{name: 'Jack', salary: 1300}]
  }
};

// The function to do the job
function sumSalaries(department) {
  if (Array.isArray(department)) { // case (1)
    return department.reduce((prev, current) => prev + current.salary, 0); // sum the array
  } else { // case (2)
    let sum = 0;
    for (let subdep of Object.values(department)) {
      sum += sumSalaries(subdep); // recursively call for subdepartments, sum the results
    }
    return sum;
  }
}

alert(sumSalaries(company)); // 7700

Code này ngắn và dễ hiểu (hy vọng?). Đó là sức mạnh của đệ quy. Nó cũng hoạt động cho bất kỳ cấp độ lồng nhau.

Đây là sơ đồ của các cuộc gọi:

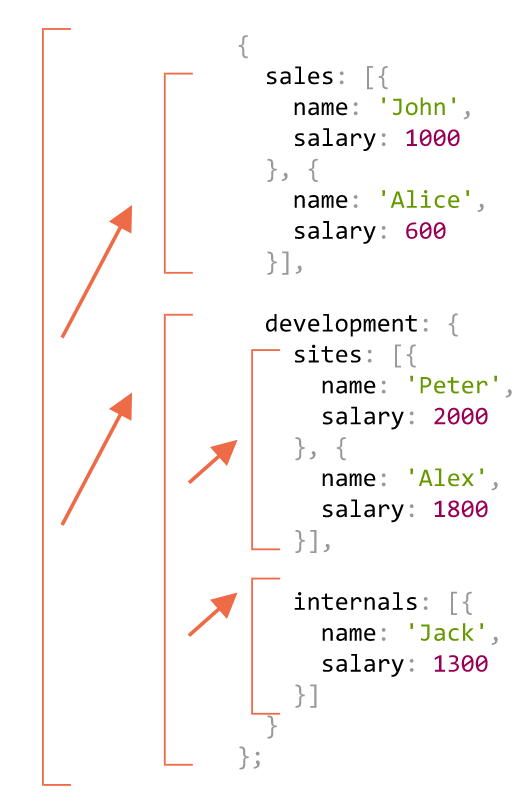
Chúng ta có thể dễ dàng thấy nguyên tắc: đối với một {...}tiểu khung đối tượng được tạo ra, trong khi các mảng [...]là các lá Lá của cây đệ quy, chúng cho kết quả ngay lập tức.

Lưu ý rằng code sử dụng các hàm thông minh mà chúng ta đã đề cập trước đây:

Phương thức được arr.reducegiải thích trong chương Phương thức mảng để lấy tổng của mảng.
Lặp lại vòng for(val of Object.values(obj))lặp trên các giá trị đối tượng: Object.valuestrả về một mảng của chúng.

4. Cấu trúc đệ quy

Cấu trúc dữ liệu đệ quy (định nghĩa đệ quy) là cấu trúc tự sao chép chính nó trong các phần.

Chúng ta vừa thấy nó trong ví dụ về cấu trúc công ty ở trên.

Một bộ phận công ty là:

Hoặc là một mảng của mọi người.
Hoặc một đối tượng với các phòng ban .

Đối với các developer web, có nhiều ví dụ nổi tiếng hơn: tài liệu HTML và XML.

Trong tài liệu HTML, thẻ HTML có thể chứa danh sách:

Văn bản mảnh.
Nhận xét HTML.
Các thẻ HTML khác (lần lượt có thể chứa các đoạn văn bản / nhận xét hoặc các thẻ khác, v.v.).

Đó là một lần nữa một định nghĩa đệ quy.

Để hiểu rõ hơn, chúng tôi sẽ trình bày thêm một cấu trúc đệ quy có tên là Danh sách liên kết có thể là một danh sách thay thế tốt hơn cho mảng trong một số trường hợp.

4.1. Linked list

Hãy tưởng tượng, chúng ta muốn lưu trữ một danh sách các đối tượng theo thứ tự.

Sự lựa chọn tự nhiên sẽ là một mảng:

let arr = [obj1, obj2, obj3];

Nhưng có một vấn đề với mảng. Xóa Các phần tử và các phần tử chèn vào các bộ phận khác rất đắt. Chẳng hạn, arr.unshift(obj)hoạt động phải đánh số lại tất cả các phần tử để nhường chỗ cho một phần mới objvà nếu mảng lớn, sẽ mất thời gian. Tương tự với arr.shift().

Các sửa đổi cấu trúc duy nhất không yêu cầu đánh số lại hàng loạt là những sửa đổi hoạt động với phần cuối của mảng : arr.push/pop. Vì vậy, một mảng có thể khá chậm đối với các hàng đợi lớn, khi chúng ta phải làm việc với sự khởi đầu.

Ngoài ra, nếu chúng ta thực sự cần chèn / xóa nhanh, chúng ta có thể chọn một cấu trúc dữ liệu khác gọi là danh sách được liên kết.

Bạn có thể tham khảo các bài viết cực chi tiết về giải thuật ở đây.

Phần tử danh sách được liên kết được định nghĩa đệ quy là một đối tượng với:

value.
nextthuộc tính tham chiếu phần tử danh sách được liên kết tiếp theo hoặc nullnếu đó là kết thúc.

Ví dụ:

let list = {
  value: 1,
  next: {
    value: 2,
    next: {
      value: 3,
      next: {
        value: 4,
        next: null
      }
    }
  }
};

Biểu diễn đồ họa của danh sách:

Một code thay thế để tạo:

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };
list.next.next.next.next = null;

Ở đây chúng ta thậm chí có thể thấy rõ hơn rằng có nhiều đối tượng, mỗi đối tượng có valuevà nextchỉ vào hàng xóm. Các listbiến là đối tượng đầu tiên trong chuỗi, vì vậy sau nextcon trỏ từ nó chúng ta có thể đạt được bất kỳ yếu tố.

Danh sách có thể dễ dàng chia thành nhiều phần và sau đó được nối lại:

let secondList = list.next.next;
list.next.next = null;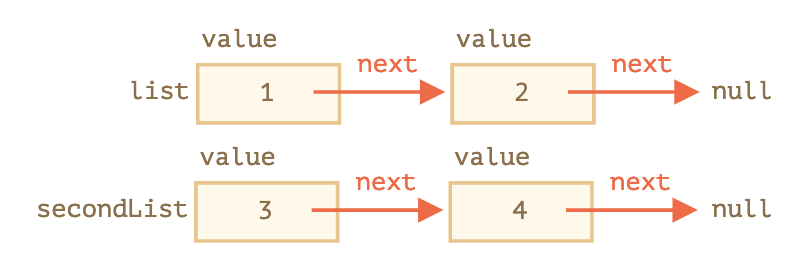

Tham gia:

list.next.next = secondList;

Và chắc chắn chúng ta có thể chèn hoặc loại bỏ các mục ở bất kỳ nơi nào.

Chẳng hạn, để thêm một giá trị mới, chúng ta cần cập nhật phần đầu của danh sách:

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };

// prepend the new value to the list
list = { value: "new item", next: list };

Để xóa một giá trị từ giữa, thay đổi giá trị nexttrước đó:

list.next = list.next.next;

Chúng ta đã list.nextnhảy qua 1giá trị 2. Giá trị 1hiện được loại trừ khỏi chuỗi. Nếu nó không được lưu trữ ở bất kỳ nơi nào khác, nó sẽ tự động bị xóa khỏi bộ nhớ.

Không giống như mảng, không có số lượng lớn, chúng ta có thể dễ dàng sắp xếp lại các phần tử.

Đương nhiên, danh sách không phải lúc nào cũng tốt hơn mảng. Nếu không mọi người sẽ chỉ sử dụng danh sách.

Hạn chế chính là chúng ta không thể dễ dàng truy cập một yếu tố bằng số của nó. Trong một mảng đó là dễ dàng: arr[n]là một tài liệu tham khảo trực tiếp. Nhưng trong danh sách, chúng ta cần bắt đầu từ mục đầu tiên và next Nthời gian để lấy phần tử Nth.

Nhưng không phải lúc nào chúng ta cũng cần những thao tác như vậy. Chẳng hạn, khi chúng ta cần một hàng đợi hoặc thậm chí là một deque – cấu trúc được sắp xếp phải cho phép thêm / xóa rất nhanh các phần tử từ cả hai đầu, nhưng không cần truy cập vào giữa của nó.

Danh sách có thể được nâng cao:

Chúng ta có thể thêm prevthuộc tính ngoài nexttham chiếu phần tử trước đó, để di chuyển trở lại dễ dàng.
Chúng ta cũng có thể thêm một biến có tên tailtham chiếu phần tử cuối cùng của danh sách (và cập nhật nó khi thêm / xóa phần tử từ cuối).
Cấu trúc dữ liệu có thể thay đổi theo nhu cầu của chúng ta.

5. Tóm lược

Điều kiện:

Đệ quy là một thuật ngữ lập trình có nghĩa là gọi một hàm từ chính nó. Các hàm đệ quy có thể được sử dụng để giải quyết các nhiệm vụ theo những cách thanh lịch. Khi một hàm tự gọi, đó gọi là bước đệ quy . Cơ sở của đệ quy là các đối số hàm làm cho tác vụ đơn giản đến mức hàm không thực hiện các cuộc gọi tiếp theo.
Một định nghĩa đệ quy cấu trúc dữ liệu là một cấu trúc dữ liệu có thể được định nghĩa bằng chính nó. Ví dụ, danh sách được liên kết có thể được định nghĩa là cấu trúc dữ liệu bao gồm một đối tượng tham chiếu danh sách (hoặc null). list = { value, next -> list }
Các cây như cây phần tử HTML hoặc cây bộ phận từ chương này cũng được đệ quy một cách tự nhiên: chúng phân nhánh và mỗi nhánh có thể có các nhánh khác. Các hàm đệ quy có thể được sử dụng để đi bộ chúng như chúng ta đã thấy trong sumSalaryví dụ.

Bất kỳ hàm đệ quy nào cũng có thể được viết lại thành một hàm lặp. Và điều đó đôi khi được yêu cầu để tối ưu hóa công cụ. Nhưng đối với nhiều tác vụ, một giải pháp đệ quy là đủ nhanh và dễ dàng hơn để viết và hỗ trợ.

Bạn có thể tham khảo các bài viết cực chi tiết về cấu trúc dữ liệu và giải thuật ở đây.

Full series tự học Javascript từ cơ bản tới nâng cao tại đây nha.

Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:

Chào thân ái và quyết thắng!

[Tự học Javascript] Đệ quy và ngăn xếp(stack), Linked list trong Javascript

1. Hai cách nghĩ

2. Bối cảnh thực hiện và ngăn xếp

2.1. pow (2, 3)

2.2. pow (2, 2)

2.3. pow (2, 1)

2.4. Lối thoát

3. Chuyển tiếp đệ quy

4. Cấu trúc đệ quy

4.1. Linked list

5. Tóm lược

Đăng ký kênh youtube để ủng hộ Cafedev nha các bạn, Thanks you!

BÀI VIẾT TIÊU BIỂU

Hiểu lỗi HTTP 431: Hướng dẫn cho nhà phát triển

Tiện ích AI Copilot sử dụng AWS Multi-Agent Orchestrator với hiệu...

Cách thiết kế Luồng Sự kiện, Phần 2: Bí quyết hấp...

BÀI VIẾT PHỔ BIẾN

Tổng hợp toàn bộ tài liệu học hướng đối tượng và...

[Tự học C++] Số dấu phẩy động(float, double,…) trong C++

Tổng hợp và chọn lọc bài tập SQL full hướng dẫn...

MỤC XEM NHIỀU