Tự học ML | Các loại kỹ thuật hồi quy(Regression)

Khi nào chọn hồi quy được chọn?

Một vấn đề hồi quy là khi biến đầu ra là một giá trị thực hoặc liên tục, chẳng hạn như “tiền lương” hoặc “trọng lượng”. Nhiều mô hình khác nhau có thể được sử dụng, đơn giản nhất là hồi quy tuyến tính. Nó cố gắng khớp dữ liệu với để dữ liệu phẳng tốt nhất đi qua các điểm.

Phân tích hồi quy là một quá trình thống kê để ước tính mối quan hệ giữa các biến phụ thuộc hoặc biến tiêu chí và một hoặc nhiều biến hoặc yếu tố dự báo độc lập. Phân tích hồi quy giải thích những thay đổi trong tiêu chí liên quan đến những thay đổi trong các yếu tố dự báo được chọn. Kỳ vọng có điều kiện của các tiêu chí dựa trên các yếu tố dự báo trong đó giá trị trung bình của các biến phụ thuộc được đưa ra khi các biến độc lập được thay đổi. Ba cách sử dụng chính để phân tích hồi quy là xác định sức mạnh của các yếu tố dự báo, dự báo hiệu ứng và dự báo xu hướng.

1. Các loại hồi quy 

• Hồi quy tuyến tính
• Hồi quy logistic
• Hồi quy đa thức
• Hồi quy từng bước
• Hồi quy từng bước
• Hồi quy Ridge
• Hồi quy Lasso
• Hồi quy ElasticNet

Hồi quy tuyến tính được sử dụng để phân tích dự đoán. Hồi quy tuyến tính là một cách tiếp cận tuyến tính để mô hình hóa mối quan hệ giữa tiêu chí hoặc phản ứng vô hướng và nhiều yếu tố dự báo hoặc biến giải thích. Hồi quy tuyến tính tập trung vào phân phối xác suất có điều kiện của phản hồi cho các giá trị của các yếu tố dự đoán. Đối với hồi quy tuyến tính, có nguy cơ trang bị quá mức. Công thức của hồi quy tuyến tính là: Y ’= bX + A.

Hồi quy logistic được sử dụng khi biến phụ thuộc có tính phân đôi. Hồi quy logistic ước tính các tham số của mô hình logistic và là dạng hồi quy nhị thức. Hồi quy logistic được sử dụng để xử lý dữ liệu có hai tiêu chí có thể có và mối quan hệ giữa tiêu chí và yếu tố dự đoán. Phương trình hồi quy logistic là: l =

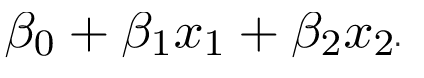
Hồi quy đa thức được sử dụng cho dữ liệu đường cong. Hồi quy đa thức phù hợp với phương pháp bình phương nhỏ nhất. Mục tiêu của phân tích hồi quy để mô hình hóa giá trị kỳ vọng của một biến phụ thuộc y liên quan đến biến độc lập x. Phương trình hồi quy đa thức là: l =

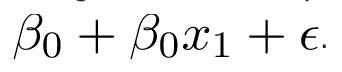
Hồi quy từng bước được sử dụng để lắp mô hình hồi quy với mô hình dự đoán. Nó được thực hiện tự động. Với mỗi bước, biến được cộng hoặc trừ khỏi tập hợp các biến giải thích. Các phương pháp tiếp cận cho hồi quy từng bước là lựa chọn tiến, loại bỏ lùi và loại bỏ hai chiều. Công thức cho hồi quy từng bước là.

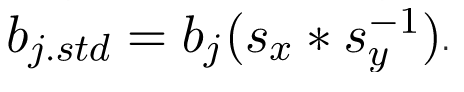
Hồi quy Ridge là một kỹ thuật để phân tích dữ liệu hồi quy nhiều lần. Khi xảy ra đa cộng tuyến, các ước lượng bình phương nhỏ nhất là không chệch. Một mức độ chệch được thêm vào các ước tính hồi quy và kết quả là hồi quy sườn núi làm giảm các sai số tiêu chuẩn. Công thức cho hồi quy sườn núi là.

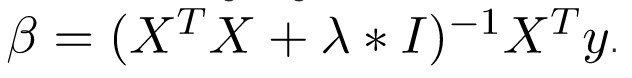
Hồi quy Lasso là một phương pháp phân tích hồi quy thực hiện cả lựa chọn biến và chính quy hóa. Hồi quy Lasso sử dụng ngưỡng mềm. Hồi quy Lasso chỉ chọn một tập hợp con của các hiệp biến được cung cấp để sử dụng trong mô hình cuối cùng. Hồi quy Lasso là.

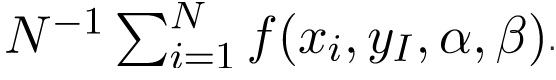
Hồi quy ElasticNet là một phương pháp hồi quy chính quy kết hợp tuyến tính các hình phạt của phương pháp lasso và phương pháp ridge. Hồi quy ElasticNet được sử dụng để hỗ trợ máy vectơ, học số liệu và tối ưu hóa danh mục đầu tư. Hàm hình phạt được cho bởi:.

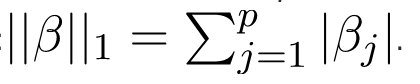
Dưới đây là cách thực hiện đơn giản:

# importing libraries 
import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.linear_model import LinearRegression 
  
x = 11 * np.random.random((10, 1)) 
  
# y = a * x + b 
y = 1.0 * x + 3.0
  
# create a linear regression model 
model = LinearRegression() 
model.fit(x, y) 
  
# predict y from the data where the x is predicted from the x 
x_pred = np.linspace(0, 11, 100) 
y_pred = model.predict(x_pred[:, np.newaxis]) 
  
# plot the results 
plt.figure(figsize =(3, 5)) 
ax = plt.axes() 
ax.scatter(x, y) 
  
ax.plot(x_pred, y_pred) 
ax.set_xlabel('predictors') 
ax.set_ylabel('criterion') 
ax.axis('tight') 
  
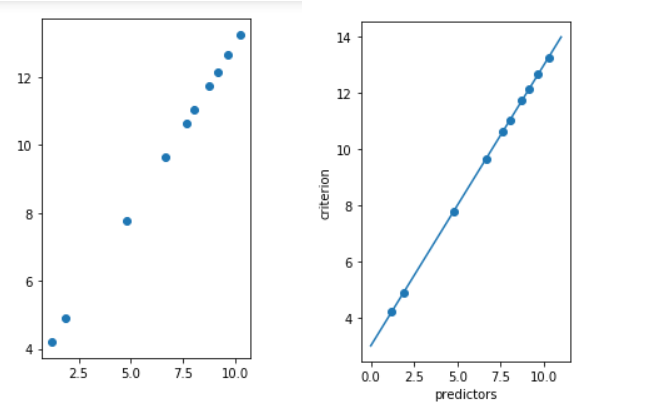
plt.show() 

Output:

Nguồn và Tài liệu tiếng anh tham khảo:

• w3school
• python.org
• geeksforgeeks

Tài liệu từ cafedev:

• Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
• Tự học ML bằng Python từ cơ bản tới nâng cao.
• Ebook về python tại đây.
• Các series tự học lập trình MIỄN PHÍ khác
• Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.

Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:

• Group Facebook
• Fanpage
• Youtube
• Instagram
• Twitter
• Linkedin
• Pinterest
• Trang chủ

Chào thân ái và quyết thắng!