Mở rộng đặc tính là một kỹ thuật để chuẩn hóa các đặc tính độc lập có trong dữ liệu trong một phạm vi cố định. Nó được thực hiện trong quá trình xử lý trước của dữ liệu.
Khi làm việc:
Đưa ra tập dữ liệu với các đặc tính – Tuổi, Lương, Căn hộ BHK với kích thước dữ liệu là 5000 người, mỗi người có các đặc tính dữ liệu độc lập này.
Mỗi điểm dữ liệu được gắn nhãn là:
- Class1 – CÓ (có nghĩa là với Giá trị đặc tính Căn hộ, Tuổi, Lương, BHK nhất định người ta có thể mua tài sản)
- Class2 – Không (có nghĩa là với Giá trị đặc tính Căn hộ, Tuổi, Lương, BHK nhất định, người ta không thể mua tài sản).
Sử dụng tập dữ liệu để đào tạo mô hình, người ta nhằm mục đích xây dựng một mô hình có thể dự đoán liệu người ta có thể mua một tài sản hay không với các giá trị đặc tính đã cho.
Sau khi mô hình được đào tạo, một biểu đồ N-chiều (trong đó N là số của các đối tượng có trong tập dữ liệu) với các điểm dữ liệu từ tập dữ liệu đã cho, có thể được tạo. Hình dưới đây là một đại diện lý tưởng của mô hình.
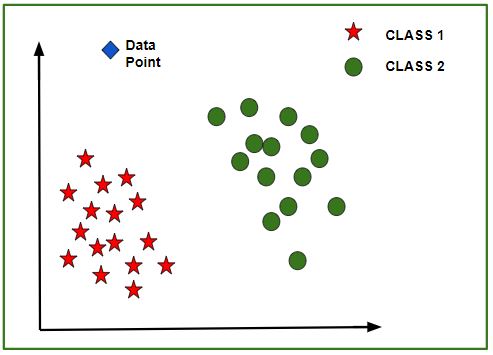
Như trong hình, các điểm dữ liệu hình sao thuộc Loại1 – Có và các vòng tròn đại diện cho Loại2 – Không có nhãn và mô hình được đào tạo bằng cách sử dụng các điểm dữ liệu này. Bây giờ một điểm dữ liệu mới (hình thoi như trong hình) được đưa ra và nó có các giá trị độc lập khác nhau cho 3 đặc điểm (Tuổi, Lương, Căn hộ BHK) nói trên. Mô hình phải dự đoán liệu điểm dữ liệu này thuộc Có hay Không.
Nội dung chính
1. Dự đoán về lớp của điểm dữ liệu mới:
Mô hình tính toán khoảng cách của điểm dữ liệu này từ tâm của mỗi nhóm lớp. Cuối cùng điểm dữ liệu này sẽ thuộc về lớp đó, sẽ có khoảng cách centroid tối thiểu so với nó.
Khoảng cách có thể được tính toán giữa centroid và điểm dữ liệu bằng cách sử dụng các phương pháp này-
- Khoảng cách Euclide: Là căn bậc hai của tổng bình phương chênh lệch giữa các tọa độ (giá trị đặc điểm – Tuổi, Lương, Căn hộ BHK) của điểm dữ liệu và tâm của mỗi lớp. Công thức này được đưa ra bởi định lý Pitago.
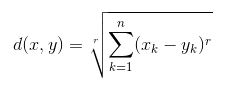
trong đó x là giá trị Điểm dữ liệu, y là giá trị Centroid và k là không. của giá trị đối tượng, Ví dụ: tập dữ liệu đã cho có k = 3
- Khoảng cách Manhattan: Nó được tính bằng tổng chênh lệch tuyệt đối giữa các tọa độ (giá trị đặc trưng) của điểm dữ liệu và tâm của mỗi lớp.
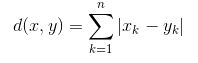
- Khoảng cách Minkowski: Là tổng quát của hai phương pháp trên. Như thể hiện trong hình, các giá trị khác nhau có thể được sử dụng để tìm r.
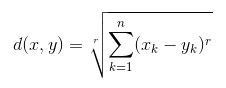
2. Cần chia việc mở rộng đặc tính:
Tập dữ liệu đã cho gồm 3 đặc điểm – Tuổi, Lương, Căn hộ BHK. Cân nhắc phạm vi 10-60 cho Tuổi, 1 Lạc- 40 Lạc cho Lương, 1-5 cho BHK Không đổi. Tất cả các đặc tính này độc lập với nhau.
Giả sử tâm của lớp 1 là [40, 22 Lacs, 3] và điểm dữ liệu được dự đoán là [57, 33 Lacs, 2].
Sử dụng phương pháp Manhattan
Distance = (|(40 - 57)| + |(2200000 - 3300000)| + |(3 - 2)|)Có thể thấy rằng đặc tính Lương sẽ chi phối tất cả các đặc tính khác trong khi dự đoán loại của điểm dữ liệu đã cho và vì tất cả các đặc tính đều độc lập với nhau nên mức lương của một người không liên quan đến tuổi của anh ta / cô ta hoặc yêu cầu của căn hộ anh ta / Cô bé có. Điều này có nghĩa là mô hình sẽ luôn dự đoán sai.
Vì vậy, giải pháp đơn giản cho vấn đề này là đặc tính Scaling. Thuật toán chia đặc tính mở rộng sẽ chia tỷ lệ Tuổi, Lương, BHK trong phạm vi cố định, chẳng hạn như [-1, 1] hoặc [0, 1]. Và sau đó không có đặc tính nào có thể thống trị khác.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
