Chúng ta được cung cấp một tập dữ liệu gồm các mục, với các tính năng nhất định và giá trị cho các đối tượng này (như vectơ). Nhiệm vụ là phân loại các mặt hàng đó thành từng nhóm. Để đạt được điều này, chúng ta sẽ sử dụng thuật toán kMeans; một thuật toán học tập không giám sát.
Nội dung chính
1. Tổng quát
(Sẽ hữu ích nếu bạn coi các mục là điểm trong không gian n chiều). Thuật toán sẽ phân loại các mục thành k nhóm giống nhau. Để tính độ tương đồng đó, chúng ta sẽ sử dụng khoảng cách euclide làm phép đo.
Các thuật toán hoạt động như sau:
Đầu tiên chúng ta khởi tạo k điểm, được gọi là phương tiện, một cách ngẫu nhiên.
Chúng tôi phân loại từng mục theo giá trị trung bình gần nhất và chúng tôi cập nhật tọa độ trung bình, là giá trị trung bình của các mục được phân loại theo giá trị đó cho đến nay.
Chúng ta lặp lại quy trình cho một số lần lặp nhất định và cuối cùng, chúng ta có các cụm của mình.
Các “điểm” được đề cập ở trên được gọi là phương tiện, vì chúng chứa các giá trị trung bình của các mục được phân loại trong đó. Để khởi tạo các phương tiện này, chúng ta có rất nhiều lựa chọn. Một phương pháp trực quan là khởi tạo phương tiện tại các mục ngẫu nhiên trong tập dữ liệu. Một phương pháp khác là khởi tạo phương tiện ở các giá trị ngẫu nhiên giữa các ranh giới của tập dữ liệu (nếu đối với một đối tượng x, các mục có giá trị bằng [0,3], chúng tôi sẽ khởi tạo phương tiện với giá trị cho x ở [0,3]) .
Thuật toán trên trong mã giả:
- Khởi tạo k nghĩa với các giá trị ngẫu nhiên
- Đối với một số lần lặp nhất định:
- Lặp lại các mục:
- Tìm giá trị gần nhất với mục
- Gán mục có nghĩa
- Cập nhật trung bình
2. Đọc dữ liệu
Chúng ta nhận đầu vào dưới dạng tệp văn bản (‘data.txt’). Mỗi dòng đại diện cho một mục và nó chứa các giá trị số (một cho mỗi đối tượng địa lý) được phân tách bằng dấu phẩy. Bạn có thể tìm thấy tập dữ liệu mẫu tại đây.
Chúng ta sẽ đọc dữ liệu từ tệp, lưu vào danh sách. Mỗi phần tử của danh sách là một danh sách khác chứa các giá trị mục cho các tính năng. Chúng tôi làm điều này với chức năng sau:
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
def ReadData(fileName):
# Read the file, splitting by lines
f = open(fileName, 'r');
lines = f.read().splitlines();
f.close();
items = [];
for i in range(1, len(lines)):
line = lines[i].split(',');
itemFeatures = [];
for j in range(len(line)-1):
# Convert feature value to float
v = float(line[j]);
# Add feature value to dict
itemFeatures.append(v);
items.append(itemFeatures);
shuffle(items);
return items; 3. Khởi tạo Means
Chúng ta muốn khởi tạo từng giá trị trung bình trong phạm vi giá trị tính năng của các mục. Để làm được điều đó, chúng ta cần tìm giá trị tối thiểu và tối đa cho từng tính năng. Chúng tôi thực hiện điều đó với chức năng sau:
def FindColMinMax(items):
n = len(items[0]);
minima = [sys.maxint for i in range(n)];
maxima = [-sys.maxint -1 for i in range(n)];
for item in items:
for f in range(len(item)):
if (item[f] < minima[f]):
minima[f] = item[f];
if (item[f] > maxima[f]):
maxima[f] = item[f];
return minima,maxima; Các biến cực tiểu, cực đại là danh sách chứa giá trị tối thiểu và giá trị lớn nhất của các mục tương ứng. Chúng tôi khởi tạo các giá trị tính năng của mỗi giá trị trung bình một cách ngẫu nhiên giữa giá trị tối thiểu và tối đa tương ứng trong hai danh sách trên:
def InitializeMeans(items, k, cMin, cMax):
# Initialize means to random numbers between
# the min and max of each column/feature
f = len(items[0]); # number of features
means = [[0 for i in range(f)] for j in range(k)];
for mean in means:
for i in range(len(mean)):
# Set value to a random float
# (adding +-1 to avoid a wide placement of a mean)
mean[i] = uniform(cMin[i]+1, cMax[i]-1);
return means; 4. Khoảng cách Euclide
Chúng ta sẽ sử dụng khoảng cách euclide làm thước đo độ tương tự cho tập dữ liệu của mình (lưu ý: tùy thuộc vào các mặt hàng của bạn, bạn có thể sử dụng một số liệu tương tự khác).
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
def EuclideanDistance(x, y):
S = 0; # The sum of the squared differences of the elements
for i in range(len(x)):
S += math.pow(x[i]-y[i], 2)
#The square root of the sum
return math.sqrt(S) 5. Cập nhật phương tiện
Để cập nhật giá trị trung bình, chúng ta cần tìm giá trị trung bình cho tính năng của nó, cho tất cả các mục trong trung bình / cụm. Chúng ta có thể làm điều này bằng cách cộng tất cả các giá trị và sau đó chia cho số mục hoặc chúng ta có thể sử dụng một giải pháp thanh lịch hơn. Chúng ta sẽ tính giá trị trung bình mới mà không cần phải cộng lại tất cả các giá trị bằng cách thực hiện như sau:
m = (m * (n-1) + x) / n
trong đó m là giá trị trung bình của một đối tượng địa lý, n là số lượng mục trong cụm và x là giá trị đối tượng địa lý cho mục được thêm vào. Chúng tôi làm như trên cho từng tính năng để có được giá trị trung bình mới.
def UpdateMean(n,mean,item):
for i in range(len(mean)):
m = mean[i];
m = (m*(n-1)+item[i])/float(n);
mean[i] = round(m, 3);
return mean;6. Phân loại các mặt hàng
Bây giờ chúng ta cần viết một hàm để phân loại một mục vào một nhóm / cụm. Đối với mặt hàng đã cho, chúng tôi sẽ tìm mức độ tương tự của nó với từng giá trị trung bình và chúng tôi sẽ phân loại mặt hàng đó cho gần nhất.
def Classify(means,item):
# Classify item to the mean with minimum distance
minimum = sys.maxint;
index = -1;
for i in range(len(means)):
# Find distance from item to mean
dis = EuclideanDistance(item, means[i]);
if (dis < minimum):
minimum = dis;
index = i;
return index; 7. Tìm phương tiện
Để thực sự tìm ra phương tiện, chúng tôi sẽ lặp lại tất cả các mục, phân loại chúng theo cụm gần nhất và cập nhật ý nghĩa của cụm. Chúng tôi sẽ lặp lại quá trình cho một số lần lặp lại cố định. Nếu giữa hai lần lặp lại không có mục nào thay đổi phân loại, chúng tôi dừng quá trình vì thuật toán đã tìm ra giải pháp tối ưu.
Hàm dưới đây nhận đầu vào là k (số cụm mong muốn), các mục và số lần lặp tối đa, trả về phương tiện và cụm. Phân loại của một mục được lưu trữ trong mảng Thuộc về và số lượng mục trong một cụm được lưu trữ trong ClusterSizes.
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
def CalculateMeans(k,items,maxIterations=100000):
# Find the minima and maxima for columns
cMin, cMax = FindColMinMax(items);
# Initialize means at random points
means = InitializeMeans(items,k,cMin,cMax);
# Initialize clusters, the array to hold
# the number of items in a class
clusterSizes= [0 for i in range(len(means))];
# An array to hold the cluster an item is in
belongsTo = [0 for i in range(len(items))];
# Calculate means
for e in range(maxIterations):
# If no change of cluster occurs, halt
noChange = True;
for i in range(len(items)):
item = items[i];
# Classify item into a cluster and update the
# corresponding means.
index = Classify(means,item);
clusterSizes[index] += 1;
cSize = clusterSizes[index];
means[index] = UpdateMean(cSize,means[index],item);
# Item changed cluster
if(index != belongsTo[i]):
noChange = False;
belongsTo[i] = index;
# Nothing changed, return
if (noChange):
break;
return means;8. Tìm cụm
Cuối cùng, chúng tôi muốn tìm các cụm, cho các phương tiện. Chúng tôi sẽ lặp lại tất cả các mục và chúng tôi sẽ phân loại từng mục vào cụm gần nhất của nó.
def FindClusters(means,items):
clusters = [[] for i in range(len(means))]; # Init clusters
for item in items:
# Classify item into a cluster
index = Classify(means,item);
# Add item to cluster
clusters[index].append(item);
return clusters; 9. Các biện pháp tương tự được sử dụng phổ biến khác là:
1. Khoảng cách cosin: Nó xác định cosin của góc giữa các vectơ điểm của hai điểm trong không gian n chiều
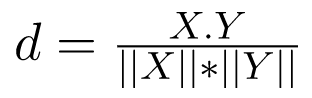
2. Khoảng cách Manhattan: Nó tính tổng chênh lệch tuyệt đối giữa tọa độ của hai điểm dữ liệu.
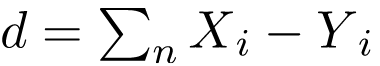
3. Khoảng cách Minkowski: Nó còn được gọi là thước đo khoảng cách tổng quát. Nó có thể được sử dụng cho cả biến thứ tự và biến định lượng
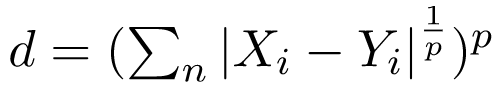
Bạn có thể tìm thấy toàn bộ mã trên GitHub của cafedev, cùng với tập dữ liệu mẫu và một hàm vẽ biểu đồ. Cảm ơn vì đã đọc.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!







![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

