Gradient Descent là một kỹ thuật tối ưu hóa được sử dụng trong các khuôn khổ ML để đào tạo các mô hình khác nhau. Quá trình đào tạo bao gồm một hàm mục tiêu (hoặc hàm lỗi), xác định lỗi mà mô hình Học máy mắc phải trên một tập dữ liệu nhất định.
Trong khi huấn luyện, các tham số của thuật toán này được khởi tạo thành các giá trị ngẫu nhiên. Khi thuật toán lặp lại, các tham số được cập nhật để chúng ta ngày càng tiến gần hơn đến giá trị tối ưu của hàm.
Tuy nhiên, Thuật toán tối ưu hóa thích ứng đang trở nên phổ biến do khả năng hội tụ nhanh chóng. Tất cả các thuật toán này, trái ngược với Gradient Descent thông thường, sử dụng số liệu thống kê từ các lần lặp trước để củng cố quá trình hội tụ.
Nội dung chính
1. Tối ưu hóa dựa trên quán tính:
Thuật toán tối ưu hóa thích ứng sử dụng các gradient trung bình có trọng số theo cấp số nhân qua các lần lặp trước để ổn định sự hội tụ, dẫn đến tối ưu hóa nhanh hơn. Ví dụ, trong hầu hết các ứng dụng thế giới thực của Mạng thần kinh, việc đào tạo được thực hiện trên dữ liệu nhiễu. Do đó, cần thiết để giảm ảnh hưởng của nhiễu khi dữ liệu được cấp theo lô trong quá trình Tối ưu hóa. Vấn đề này có thể được giải quyết bằng cách sử dụng Đường trung bình có trọng số theo cấp số nhân (hoặc Đường trung bình có trọng số theo cấp số nhân).
2. Thực hiện trung bình có trọng số theo cấp số nhân:
Để ước tính xu hướng trong tập dữ liệu nhiễu có kích thước N:
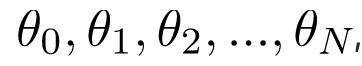
, chúng ta duy trì một tập hợp các tham số:
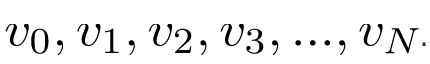
Khi chúng ta lặp lại tất cả các giá trị trong tập dữ liệu, chúng ta tính toán các tham số như sau:
Trên lần lặp t:
Tiếp theo 0t

Thuật toán này tính trung bình giá trị của V0 hơn các giá trị của nó từ các lần lặp 1/(1-B
) trước. Mức trung bình này đảm bảo rằng chỉ có xu hướng được giữ lại và tiếng ồn được tính trung bình. Phương pháp này được sử dụng như một chiến lược trong quá trình giảm độ dốc dựa trên động lượng để làm cho nó mạnh mẽ chống lại nhiễu trong các mẫu dữ liệu, dẫn đến việc đào tạo nhanh hơn.
Ví dụ: nếu bạn tối ưu hóa một hàm f(x) trên tham số x, đoạn mã giả sau minh họa thuật toán:
Trên lần lặp t:
Trên lô hiện tại
hãy tính
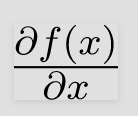
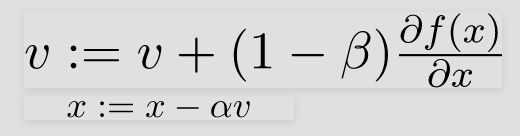
HyperParameters cho Thuật toán Tối ưu hóa này là anpla, được gọi là Tỷ lệ Học tập và, beta tương tự như gia tốc trong cơ học.
Sau đây là triển khai Gradient Descent dựa trên Momentum trên một hàm
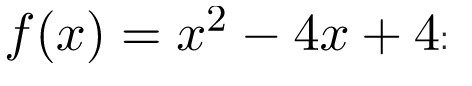
import math
# HyperParameters of the optimization algorithm
alpha = 0.01
beta = 0.9
# Objective function
def obj_func(x):
return x * x - 4 * x + 4
# Gradient of the objective function
def grad(x):
return 2 * x - 4
# Parameter of the objective function
x = 0
# Number of iterations
iterations = 0
v = 0
while (1):
iterations += 1
v = beta * v + (1 - beta) * grad(x)
x_prev = x
x = x - alpha * v
print("Value of objective function on iteration", iterations, "is", x)
if x_prev == x:
print("Done optimizing the objective function. ")
breakCài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)
