🔥CHỌN LỌC TOP NHỮNG KHOÁ HỌC LẬP TRÌNH ONLINE NHIỀU NGƯỜI THEO HOC TẠI ĐÂY🔥

Trong hồi quy tuyến tính, mô hình nhắm mục tiêu để có được đường hồi quy phù hợp nhất để dự đoán giá trị của y dựa trên giá trị đầu vào (x) đã cho. Trong khi đào tạo mô hình, mô hình sẽ tính toán chi phí của hàm đo sai số Bình phương trung bình giữa giá trị dự đoán (trước) và giá trị thực (y). Mô hình nhắm mục tiêu giảm thiểu chi phí của hàm.

Để tối thiểu hóa chi phí của hàm, mô hình cần có giá trị tốt nhất là? 1 và? 2. Ban đầu, mô hình chọn các giá trị? 1 và? 2 một cách ngẫu nhiên và sau đó cập nhật các giá trị này để giảm thiểu chi phí của hàm cho đến khi nó đạt đến mức tối thiểu. Theo thời gian mô hình đạt được hàm chi phí tối thiểu, nó sẽ có giá trị? 1 và? 2 tốt nhất. Sử dụng các giá trị cuối cùng được cập nhật này là? 1 và? 2 trong phương trình giả thuyết của phương trình tuyến tính, mô hình dự đoán giá trị của y theo cách tốt nhất có thể.

Do đó, câu hỏi được đặt ra – Làm thế nào? 1 và? 2 giá trị được cập nhật?

1. Chi phí hàm hồi quy tuyến tính:

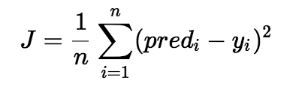
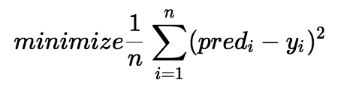
Thuật toán giảm dần độ dốc cho hồi quy tuyến tính

->? j: Trọng số của giả thuyết.
-> h? (xi): giá trị y dự đoán cho đầu vào thứ i.
-> j: Chỉ số đặc trưng (có thể là 0, 1, 2, ......, n).
->? : Tỷ lệ học tập của Gradient Descent.

Chúng ta vẽ đồ thị hàm chi phí dưới dạng một hàm ước lượng tham số, tức là phạm vi tham số của hàm giả thuyết của chúng ta và chi phí phát sinh từ việc chọn một bộ tham số cụ thể. Chúng ta di chuyển xuống phía dưới đối với các hố trong biểu đồ, để tìm giá trị nhỏ nhất. Cách để làm điều này là lấy đạo hàm của chi phí của hàm như được giải thích trong hình trên. Bước Gradient Descent giảm chi phí của hàm theo hướng dốc xuống. Kích thước của mỗi bước được xác định bằng tham số? được gọi là Tỷ lệ học tập.

2. Trong thuật toán Gradient Descent, người ta có thể suy ra hai điểm:

Nếu hệ số góc is + ve: ?J =?J – (giá trị +ve). Do đó giá trị của? J giảm.

Nếu độ dốc is -ve: ?J =?J – (giá trị -ve). Do đó giá trị của? J tăng lên.

Việc lựa chọn tỷ lệ học tập chính xác là rất quan trọng vì nó đảm bảo rằng Gradient Descent hội tụ trong một thời gian hợp lý. :

  1. Nếu chúng ta chọn ? rất lớn, Gradient Descent có thể vượt quá mức tối thiểu. Nó có thể không hội tụ hoặc thậm chí phân kỳ.

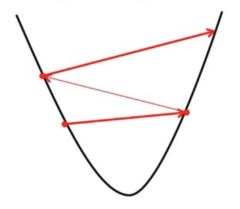
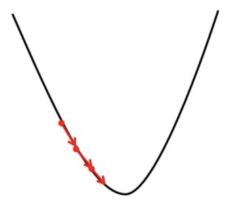
2. Nếu chúng ta chọn ? ở mức rất nhỏ, Gradient Descent sẽ thực hiện các bước nhỏ để đạt đến cực tiểu cục bộ và sẽ mất nhiều thời gian hơn để đạt cực tiểu.

Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.

Nguồn và Tài liệu tiếng anh tham khảo:

Tài liệu từ cafedev:

Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:

Chào thân ái và quyết thắng!

Đăng ký kênh youtube để ủng hộ Cafedev nha các bạn, Thanks you!

BÀI VIẾT LIÊN QUANXEM THÊM