Điều kiện tiên quyết: K-Means Clustering
Bước cơ bản đối với bất kỳ thuật toán không được giám sát nào là xác định số lượng các cụm tối ưu mà dữ liệu có thể được gom vào. Phương pháp Elbow là một trong những phương pháp phổ biến nhất để xác định giá trị tối ưu của k.
Bây giờ chúng ta chứng minh phương pháp đã cho bằng kỹ thuật phân cụm K-Means bằng cách sử dụng thư viện Sklearn của python.
Bước 1: Nhập các thư viện bắt buộc
from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
import numpy as np
import matplotlib.pyplot as plt Bước 2: Tạo và trực quan hóa dữ liệu
#Creating the data
x1 = np.array([3, 1, 1, 2, 1, 6, 6, 6, 5, 6, 7, 8, 9, 8, 9, 9, 8])
x2 = np.array([5, 4, 5, 6, 5, 8, 6, 7, 6, 7, 1, 2, 1, 2, 3, 2, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
#Visualizing the data
plt.plot()
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Dataset')
plt.scatter(x1, x2)
plt.show()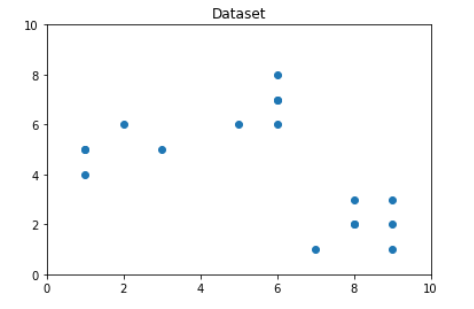 
Từ hình dung ở trên, chúng ta có thể thấy rằng số lượng cụm tối ưu nên vào khoảng 3. Nhưng trực quan hóa dữ liệu không phải lúc nào cũng đưa ra câu trả lời đúng. Do đó, chúng tôi chứng minh các bước sau.
Bây giờ chúng ta xác định như sau:
- Độ méo: Nó được tính bằng giá trị trung bình của các khoảng cách bình phương từ các tâm cụm của các cụm tương ứng. Thông thường, số liệu khoảng cách Euclide được sử dụng.
- Quán tính: Là tổng bình phương khoảng cách của các mẫu đến trung tâm cụm gần nhất của chúng.
Ta lặp lại các giá trị của k từ 1 đến 9 và tính các giá trị của độ méo cho mỗi giá trị của k và tính độ méo và quán tính cho từng giá trị của k trong khoảng đã cho.
Bước 3: Xây dựng mô hình phân cụm và tính toán các giá trị của Biến dạng và Quán tính
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
m
distortions = []
inertias = []
mapping1 = {}
mapping2 = {}
K = range(1,10)
for k in K:
#Building and fitting the model
kmeanModel = KMeans(n_clusters=k).fit(X)
kmeanModel.fit(X)
distortions.append(sum(np.min(cdist(X, kmeanModel.cluster_centers_,
'euclidean'),axis=1)) / X.shape[0])
inertias.append(kmeanModel.inertia_)
mapping1[k] = sum(np.min(cdist(X, kmeanModel.cluster_centers_,
'euclidean'),axis=1)) / X.shape[0]
mapping2[k] = kmeanModel.inertia_ Bước 4: Lập bảng và hình dung kết quả
a) Sử dụng các giá trị khác nhau của Độ méo
for key,val in mapping1.items():
print(str(key)+' : '+str(val))
b) Sử dụng các giá trị khác nhau của Quán tính
for key,val in mapping2.items():
print(str(key)+' : '+str(val)) 
plt.plot(K, distortions, 'bx-')
plt.xlabel('Values of K')
plt.ylabel('Distortion')
plt.title('The Elbow Method using Distortion')
plt.show()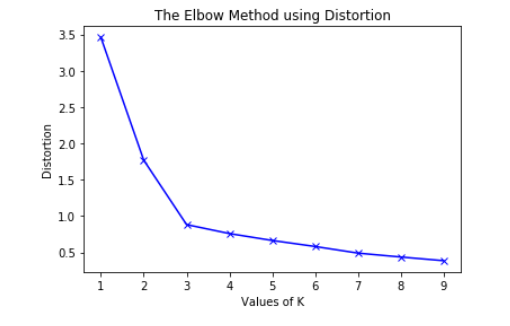
Để xác định số lượng cụm tối ưu, chúng ta phải chọn giá trị của k tại “khuỷu tay” tức là điểm mà sau đó biến dạng / quán tính bắt đầu giảm theo kiểu tuyến tính. Do đó đối với dữ liệu đã cho, chúng tôi kết luận rằng số cụm tối ưu cho dữ liệu là 3.
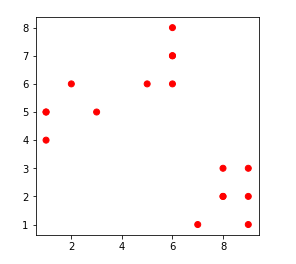
Các điểm dữ liệu được phân nhóm cho giá trị khác nhau của k:
1. k = 1
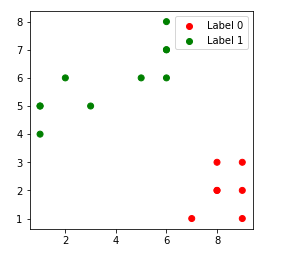
2. k = 2
3. k = 3
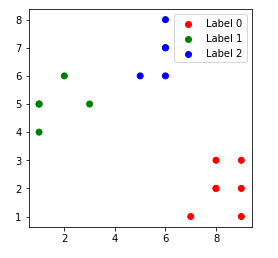
4. k = 4
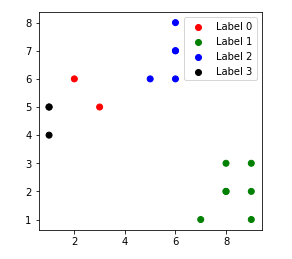
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
