Bài viết này cafedev sẽ thảo luận về lý thuyết đằng sau các bộ phân loại Naive Bayes và việc triển khai chúng.
Bộ phân loại Naive Bayes là tập hợp các thuật toán phân loại dựa trên Định lý Bayes. Nó không phải là một thuật toán đơn lẻ mà là một họ các thuật toán mà tất cả chúng đều có chung một nguyên tắc, tức là mọi cặp đặc tính được phân loại là độc lập với nhau.
Để bắt đầu, chúng ta hãy xem xét một tập dữ liệu.
Hãy xem xét một tập dữ liệu hư cấu mô tả các điều kiện thời tiết để chơi gôn. Với điều kiện thời tiết, mỗi bộ phân loại các điều kiện là phù hợp (“Có”) hoặc không phù hợp (“Không”) để đánh gôn.
Đây là phần trình bày dạng bảng của tập dữ liệu của chúng ta.
OUTLOOK | TEMPERATURE | HUMIDITY | WINDY | PLAY GOLF | |
|---|---|---|---|---|---|
| 0 | Rainy | Hot | High | False | No |
| 1 | Rainy | Hot | High | True | No |
| 2 | Overcast | Hot | High | False | Yes |
| 3 | Sunny | Mild | High | False | Yes |
| 4 | Sunny | Cool | Normal | False | Yes |
| 5 | Sunny | Cool | Normal | True | No |
| 6 | Overcast | Cool | Normal | True | Yes |
| 7 | Rainy | Mild | High | False | No |
| 8 | Rainy | Cool | Normal | False | Yes |
| 9 | Sunny | Mild | Normal | False | Yes |
| 10 | Rainy | Mild | Normal | True | Yes |
| 11 | Overcast | Mild | High | True | Yes |
| 12 | Overcast | Hot | Normal | False | Yes |
| 13 | Sunny | Mild | High | True | No |
Tập dữ liệu được chia thành hai phần, đó là ma trận đặc trưng và vectơ phản hồi.
- Ma trận đối tượng chứa tất cả các vectơ (hàng) của tập dữ liệu, trong đó mỗi vectơ bao gồm giá trị của các đối tượng phụ thuộc. Trong tập dữ liệu trên, các tính năng là ‘Outlook’, ‘Nhiệt độ’, ‘Độ ẩm’ và ‘Có gió’.
- Vectơ phản hồi chứa giá trị của biến lớp (dự đoán hoặc đầu ra) cho mỗi hàng của ma trận đặc trưng. Trong tập dữ liệu trên, tên biến lớp là ‘Chơi gôn’.
Nội dung chính
1. Giả thiết:
Giả định cơ bản của Naive Bayes là mỗi tính năng tạo nên:
- độc lập
- công bằng
đóng góp vào kết quả.
Với mối quan hệ với tập dữ liệu của chúng ta, khái niệm này có thể được hiểu là:
- Chúng ta giả định rằng không có cặp tính năng nào là phụ thuộc. Ví dụ: nhiệt độ là “Nóng” không liên quan gì đến độ ẩm hoặc triển vọng là “Mưa” không ảnh hưởng đến gió. Do đó, các tính năng được giả định là độc lập.
- Thứ hai, mỗi tính năng có cùng trọng số (hoặc tầm quan trọng). Ví dụ: chỉ biết nhiệt độ và độ ẩm không thể dự đoán chính xác kết quả. Không có thuộc tính nào là không liên quan và được cho là đóng góp như nhau vào kết quả.
Lưu ý: Các giả định do Naive Bayes đưa ra thường không đúng trong các tình huống thực tế. Trên thực tế, giả định về tính độc lập không bao giờ đúng nhưng thường hoạt động tốt trong thực tế.
Bây giờ, trước khi chuyển sang công thức cho Naive Bayes, điều quan trọng là phải biết về định lý Bayes.
2, Định lý Bayes
Định lý Bayes tìm xác suất của một sự kiện xảy ra với xác suất của một sự kiện khác đã xảy ra. Định lý Bayes được phát biểu về mặt toán học dưới dạng phương trình sau:
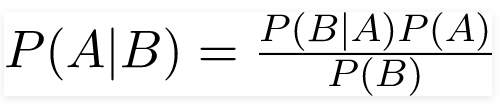
trong đó A và B là các sự kiện và P (B)? 0.
- Về cơ bản, chúng ta đang cố gắng tìm xác suất của sự kiện A, với điều kiện sự kiện B là đúng. Sự kiện B cũng được gọi là bằng chứng.
- P (A) là tiên nghiệm của A (xác suất trước, tức là xác suất của sự kiện trước khi bằng chứng được nhìn thấy). Bằng chứng là một giá trị thuộc tính của một cá thể không xác định (ở đây, nó là sự kiện B).
- P (A | B) là xác suất hậu kỳ của B, tức là xác suất của sự kiện sau khi bằng chứng được nhìn thấy.
Bây giờ, liên quan đến tập dữ liệu của chúng ta, chúng ta có thể áp dụng định lý Bayes theo cách sau:
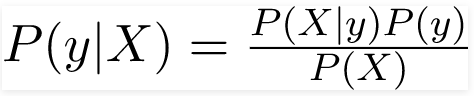
trong đó, y là biến lớp và X là vectơ đặc trưng phụ thuộc (có kích thước n) trong đó:
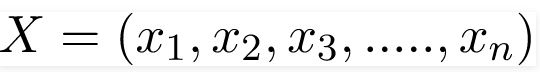
Chỉ để rõ ràng, một ví dụ về vectơ đặc trưng và biến lớp tương ứng có thể là: (tham khảo hàng đầu tiên của tập dữ liệu)
X = (Rainy, Hot, High, False)
y = NoVì vậy, về cơ bản, P (y | X) ở đây có nghĩa là, xác suất “Không chơi gôn” với điều kiện thời tiết là “Có mưa”, “Nhiệt độ nóng”, “độ ẩm cao” và “không có gió”.
3. Giả định Naive
Bây giờ, đã đến lúc đặt một giả định Naive cho định lý Bayes, tức là sự độc lập giữa các đối tượng địa lý. Vì vậy, bây giờ, chúng ta chia bằng chứng thành các phần độc lập.
Bây giờ, nếu hai sự kiện A và B bất kỳ là độc lập, thì
P (A, B) = P (A) P (B)
Do đó, chúng tôi đạt được kết quả:
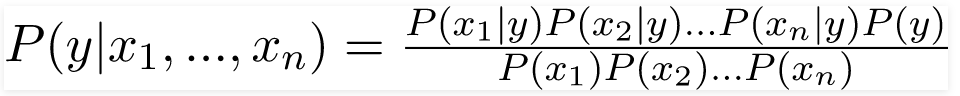
có thể được diễn đạt như sau:
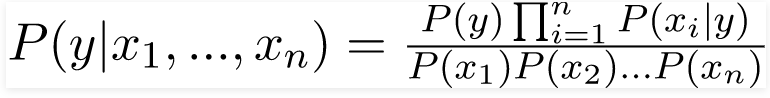
Bây giờ, vì mẫu số không đổi đối với một đầu vào nhất định, chúng ta có thể loại bỏ thuật ngữ đó:
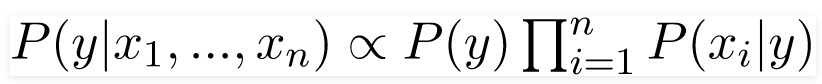
Bây giờ, chúng ta cần tạo một mô hình phân loại. Đối với điều này, chúng ta tìm xác suất của bộ đầu vào đã cho cho tất cả các giá trị có thể có của biến lớp y và chọn đầu ra với xác suất tối đa. Điều này có thể được biểu thị bằng toán học như sau:
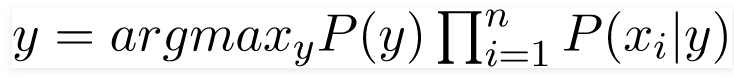
Vì vậy, cuối cùng, chúng ta chỉ còn lại nhiệm vụ tính P (y) và P (xi | y).
Xin lưu ý rằng P (y) còn được gọi là xác suất lớp và P (xi | y) được gọi là xác suất có điều kiện.
Các bộ phân loại Naive Bayes khác nhau chủ yếu khác nhau bởi các giả định mà chúng đưa ra liên quan đến phân phối P (xi | y).
Hãy để chúng ta thử áp dụng công thức trên theo cách thủ công trên tập dữ liệu thời tiết của chúng ta. Đối với điều này, chúng ta cần thực hiện một số tính toán trước trên tập dữ liệu của mình.
Chúng ta cần tìm P (xi | yj) cho mỗi xi trong X và yj trong y. Tất cả những tính toán này đã được chứng minh trong bảng dưới đây:
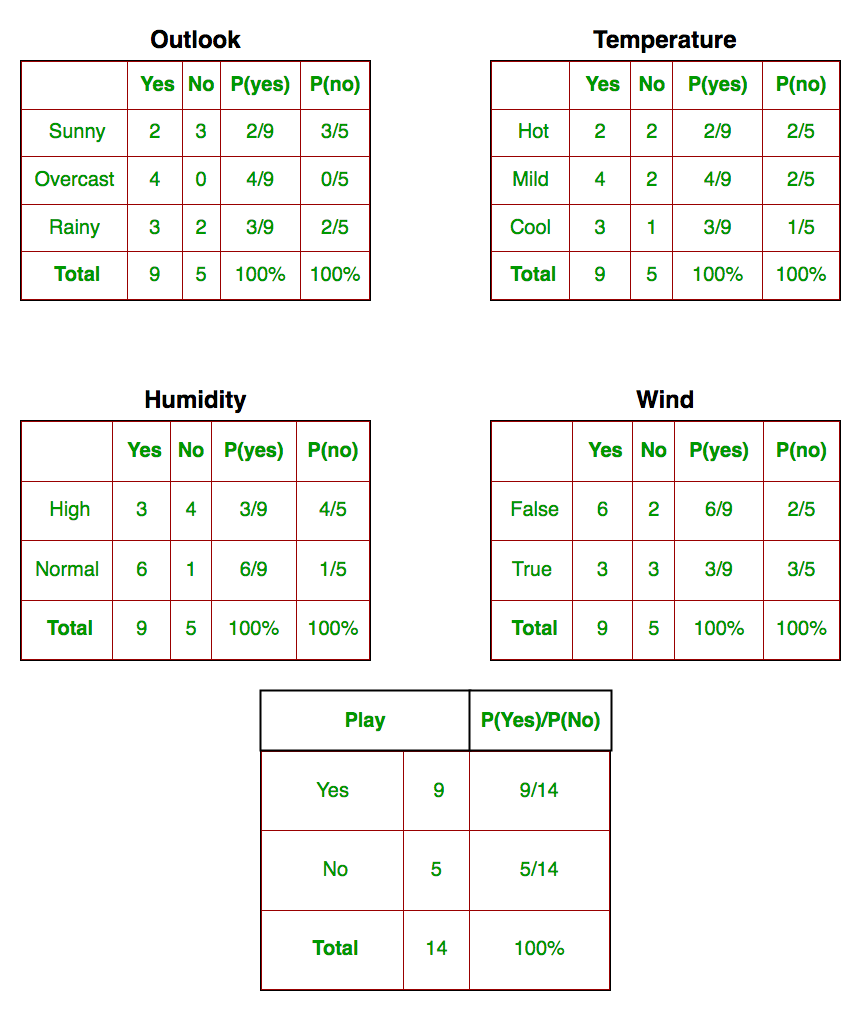
Vì vậy, trong hình trên, chúng ta đã tính toán P (xi | yj) cho mỗi xi trong X và yj trong y theo cách thủ công trong bảng 1-4. Ví dụ, xác suất chơi gôn cho rằng nhiệt độ mát, tức là P (nhiệt độ = mát | chơi gôn = Có) = 3/9.
Ngoài ra, chúng ta cần tìm xác suất của lớp (P (y)) đã được tính trong bảng 5. Ví dụ, P (chơi gôn = Có) = 9/14.
Vì vậy, bây giờ, chúng tôi đã hoàn tất các tính toán trước của mình và trình phân loại đã sẵn sàng!
Hãy để chúng ta thử nghiệm nó trên một bộ tính năng mới (chúng ta gọi nó là hôm nay):
today = (Sunny, Hot, Normal, False)
Vì vậy, xác suất chơi gôn được cho bởi:

và xác suất để không chơi gôn được cho bởi:
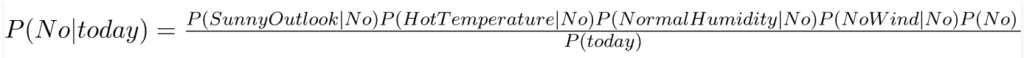
Vì P (ngày nay) là chung trong cả hai xác suất, chúng ta có thể bỏ qua P (ngày nay) và tìm xác suất tỷ lệ thuận là:
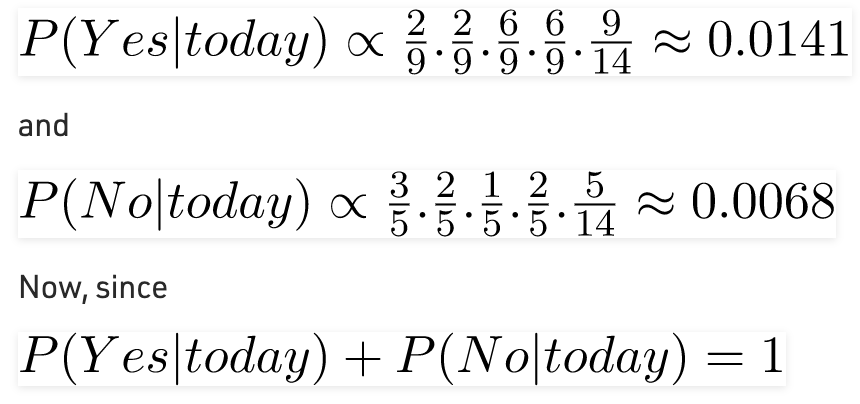
Những con số này có thể được chuyển đổi thành xác suất bằng cách làm cho tổng bằng 1 (chuẩn hóa):

Vì vậy, dự đoán rằng chơi gôn sẽ được chơi là “Có”.
Phương pháp mà chúng ta đã thảo luận ở trên có thể áp dụng cho dữ liệu rời rạc. Trong trường hợp dữ liệu liên tục, chúng ta cần đưa ra một số giả định liên quan đến việc phân phối các giá trị của từng đối tượng địa lý. Các bộ phân loại Naive Bayes khác nhau chủ yếu khác nhau bởi các giả định mà chúng đưa ra liên quan đến phân phối P (xi | y).
Bây giờ, chúng ta thảo luận về một trong những bộ phân loại như vậy ở đây.
3. Bộ phân loại Gaussian Naive Bayes
Trong Gaussian Naive Bayes, các giá trị liên tục được liên kết với mỗi đối tượng địa lý được giả định là phân phối theo phân phối Gauss. Phân phối Gaussian còn được gọi là phân phối Chuẩn. Khi được vẽ, nó cho một đường cong hình chuông đối xứng về giá trị trung bình của các giá trị đối tượng như hình dưới đây:
Khả năng của các đối tượng được giả định là Gaussian, do đó, xác suất có điều kiện được đưa ra bởi:
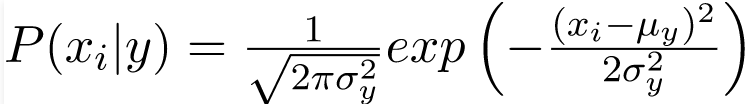
Bây giờ, chúng ta xem xét việc triển khai trình phân loại Gaussian Naive Bayes bằng cách sử dụng scikit-learning.
# load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()
# store the feature matrix (X) and response vector (y)
X = iris.data
y = iris.target
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# training the model on training set
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train, y_train)
# making predictions on the testing set
y_pred = gnb.predict(X_test)
# comparing actual response values (y_test) with predicted response values (y_pred)
from sklearn import metrics
print("Gaussian Naive Bayes model accuracy(in %):", metrics.accuracy_score(y_test, y_pred)*100)
Output
Gaussian Naive Bayes model accuracy(in %): 95.0Các bộ phân loại Naive Bayes phổ biến khác là:
- Đa thức Naive Bayes: Các vectơ đặc trưng đại diện cho các tần số mà các sự kiện nhất định đã được tạo ra bởi một phân phối đa thức. Đây là mô hình sự kiện thường được sử dụng để phân loại tài liệu.
- Bernoulli Naive Bayes: Trong mô hình sự kiện Bernoulli đa biến, các đặc trưng là các boolean độc lập (biến nhị phân) mô tả đầu vào. Giống như mô hình đa thức, mô hình này phổ biến cho các nhiệm vụ phân loại tài liệu, trong đó các tính năng xuất hiện thuật ngữ nhị phân (tức là một từ xuất hiện trong tài liệu hoặc không) được sử dụng thay vì tần suất thuật ngữ (tức là tần suất của một từ trong tài liệu).
Khi chúng ta đi đến phần cuối của bài viết này, đây là một số điểm quan trọng cần suy ngẫm:
- Bất chấp những giả định được đơn giản hóa quá mức của họ, bộ phân loại Naive Bayes đã hoạt động khá tốt trong nhiều tình huống thực tế, nổi tiếng là phân loại tài liệu và lọc thư rác. Chúng yêu cầu một lượng nhỏ dữ liệu huấn luyện để ước tính các thông số cần thiết.
- Người học và phân loại Naive Bayes có thể cực kỳ nhanh so với các phương pháp phức tạp hơn. Việc tách các phân phối đặc trưng có điều kiện của lớp có nghĩa là mỗi phân phối có thể được ước tính độc lập như một phân phối một chiều. Điều này lần lượt giúp giảm bớt các vấn đề bắt nguồn từ lời nguyền về chiều không gian.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!







![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)

