Bài viết này cafedev sẽ thảo luận về những kiến thức cơ bản của Logistic Regression và cách triển khai nó trong Python. Hồi quy logistic về cơ bản là một thuật toán phân loại có giám sát. Trong một bài toán phân loại, biến mục tiêu (hoặc đầu ra), y, chỉ có thể nhận các giá trị rời rạc cho tập hợp các đặc điểm (hoặc đầu vào) X đã cho.
Trái với suy nghĩ thông thường, hồi quy logistic LÀ một mô hình hồi quy. Mô hình xây dựng một mô hình hồi quy để dự đoán xác suất mà một mục nhập dữ liệu đã cho thuộc danh mục được đánh số là “1”. Cũng giống như hồi quy tuyến tính giả định rằng dữ liệu tuân theo một hàm tuyến tính, hồi quy Logistic mô hình hóa dữ liệu bằng cách sử dụng hàm sigmoid.
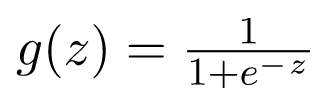
Hồi quy logistic chỉ trở thành một kỹ thuật phân loại khi một ngưỡng quyết định được đưa vào bức tranh. Việc thiết lập giá trị ngưỡng là một khía cạnh rất quan trọng của hồi quy Logistic và phụ thuộc vào chính vấn đề phân loại.
Quyết định cho giá trị của giá trị ngưỡng bị ảnh hưởng chủ yếu bởi các giá trị của độ chính xác và thu hồi. Lý tưởng nhất là chúng ta muốn cả độ chính xác và thu hồi bằng 1, nhưng trường hợp này hiếm khi xảy ra. Trong trường hợp cân bằng Độ chính xác-Thu hồi, chúng ta sử dụng các đối số sau để quyết định khi lại ngưỡng:
1. Độ chính xác thấp / Nhớ lại cao: Trong các ứng dụng mà chúng ta muốn giảm số lượng âm tính giả mà không nhất thiết phải giảm số lượng âm tính giả, chúng ta chọn giá trị quyết định có giá trị Độ chính xác thấp hoặc giá trị cao của Gọi lại. Ví dụ: trong một ứng dụng chẩn đoán ung thư, chúng ta không muốn bất kỳ bệnh nhân bị ảnh hưởng nào được phân loại là không bị ảnh hưởng mà không cần chú ý nhiều đến nếu bệnh nhân bị chẩn đoán sai là mắc bệnh ung thư. Điều này là do, sự vắng mặt của bệnh ung thư có thể được phát hiện bởi các bệnh nội khoa khác nhưng sự hiện diện của bệnh không thể được phát hiện ở một ứng viên đã bị loại.
2. Độ chính xác cao / độ thu hồi thấp: Trong các ứng dụng mà chúng ta muốn giảm số lượng âm tính giả mà không nhất thiết phải giảm số lượng âm tính giả, chúng tôi chọn giá trị quyết định có giá trị Độ chính xác cao hoặc giá trị thấp của giá trị Nhớ lại. Ví dụ: nếu chúng tôi đang phân loại khách hàng xem họ sẽ phản ứng tích cực hay tiêu cực với một quảng cáo được cá nhân hóa, chúng ta muốn hoàn toàn chắc chắn rằng khách hàng sẽ phản ứng tích cực với quảng cáo đó bởi vì nếu không, phản ứng tiêu cực có thể gây ra mất khả năng bán hàng từ khách hàng .
Dựa trên số lượng danh mục, hồi quy Logistic có thể được phân loại thành:
- nhị thức: biến mục tiêu chỉ có thể có 2 loại có thể có: “0” hoặc “1” có thể đại diện cho “thắng” so với “thua”, “đạt” so với “thất bại”, “chết” so với “còn sống”, v.v.
- đa thức: biến mục tiêu có thể có 3 hoặc nhiều loại khả dĩ không được sắp xếp theo thứ tự (tức là các loại không có ý nghĩa định lượng) như “bệnh A” so với “bệnh B” và “bệnh C”.
- thứ tự: nó xử lý các biến mục tiêu với các danh mục có thứ tự. Ví dụ, một điểm kiểm tra có thể được phân loại là: “rất kém”, “kém”, “tốt”, “rất tốt”. Ở đây, mỗi loại có thể được cho điểm như 0, 1, 2, 3.
Trước hết, chúng ta tìm hiểu dạng đơn giản nhất của hồi quy logistic, tức là hồi quy logistic nhị thức.
Nội dung chính
1. Hồi quy logistic nhị thức
Hãy xem xét một tập dữ liệu ví dụ ánh xạ số giờ học với kết quả của một kỳ thi. Kết quả chỉ có thể nhận hai giá trị, cụ thể là được truyền (1) hoặc không thành công (0):
| HOURS(X) | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 3.75 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vượt qua(Y) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Vậy, chúng ta có:
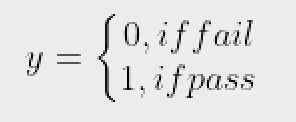
nghĩa là y là một biến mục tiêu phân loại chỉ có thể nhận hai loại có thể có: “0” hoặc “1”.
Để tổng quát hóa mô hình của chúng tôi, chúng ta giả định rằng:
- Tập dữ liệu có các biến đặc trưng ‘p’ và ‘n’ quan sát.
- Ma trận đặc điểm được biểu diễn dưới dạng:

Ở đây, Xịj biểu thị các giá trị j^th của đối tượng để quan sát i^th.
Ở đây, chúng ta đang giữ quy ước cho phép Xi0 = 1. (Hãy tiếp tục đọc, bạn sẽ hiểu logic sau một vài giây).
Quan sát i^th, Xi có thể được biểu diễn như sau:

h(xi) đại diện cho phản ứng dự đoán cho quan sát i^th, tức là. Công thức Xi chúng ta sử dụng để tính toán h(xi) được gọi là giả thuyết.
Nếu bạn đã sử dụng Hồi quy tuyến tính, bạn nên nhớ rằng trong Hồi quy tuyến tính, giả thuyết chúng ta sử dụng để dự đoán là:
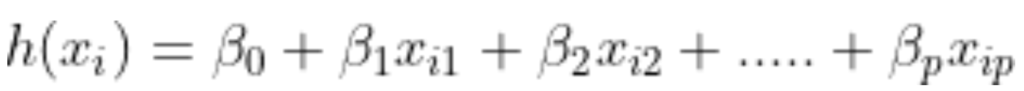
các hệ số hồi quy b0,b1,b2,…bp ở đâu.
Cho ma trận hệ số hồi quy / vectơ, B là:
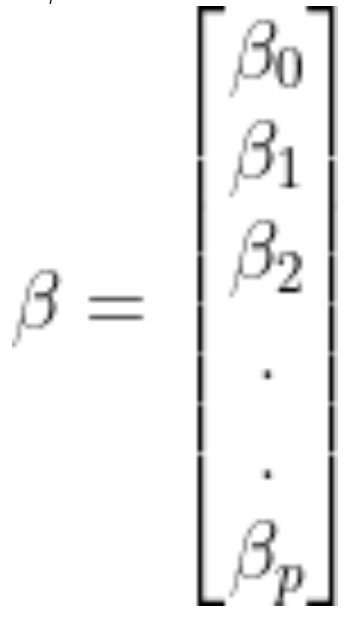
Sau đó, ở dạng nhỏ gọn hơn,
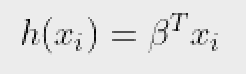
Lý do của việc lấy X0 = 1 hiện đã khá rõ ràng.
Chúng tôi cần làm một sản phẩm ma trận, nhưng không có
thực tế X0 nhân với công thức B0 giả thuyết ban đầu. Vì vậy, chúng ta đã xác định X0 = 1.
Bây giờ, nếu chúng ta cố gắng áp dụng Hồi quy tuyến tính cho bài toán trên, chúng ta có khả năng nhận được các giá trị liên tục bằng cách sử dụng giả thuyết mà chúng ta đã thảo luận ở trên. Ngoài ra, nó không có ý nghĩa cho h(xi) lấy các giá trị lớn hơn 1 hoặc nhỏ hơn 0 cũng không hợp lý.
Vì vậy, một số sửa đổi được thực hiện đối với giả thuyết để phân loại:
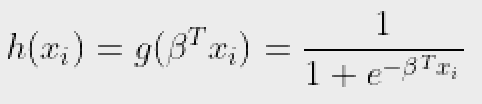
Ở đâu,
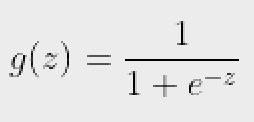
được gọi là hàm logistic hoặc hàm sigmoid.
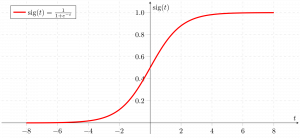
Đây là biểu đồ thể hiện g (z):
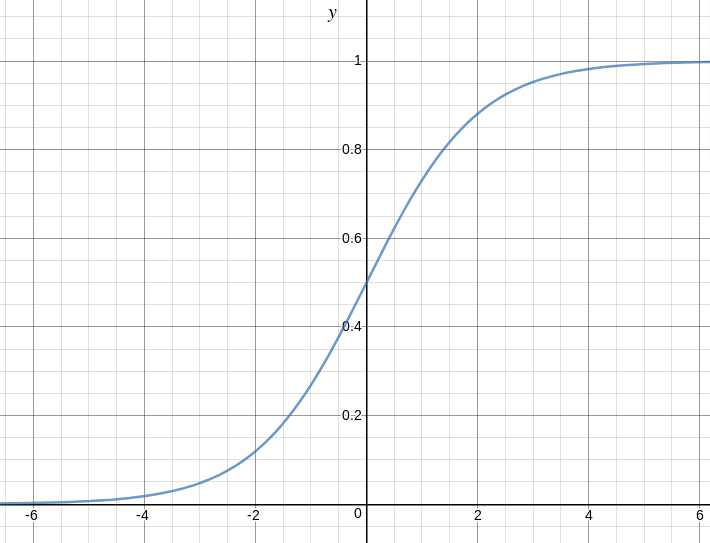
Từ biểu đồ trên, chúng ta có thể suy ra rằng:
- g (z) có xu hướng hướng tới 1 như Z -> vô cùng
- g (z) có xu hướng về 0 khi Z -> vô cùng
- g (z) luôn bị giới hạn từ 0 đến 1
Vì vậy, bây giờ, chúng ta có thể xác định các xác suất có điều kiện cho 2 nhãn (0 và 1) để quan sát như:
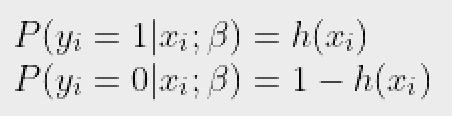
Chúng ta có thể viết gọn hơn là:
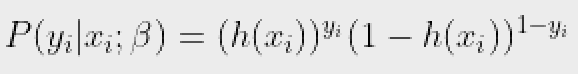
Bây giờ, chúng ta xác định một thuật ngữ khác, khả năng của các tham số là:
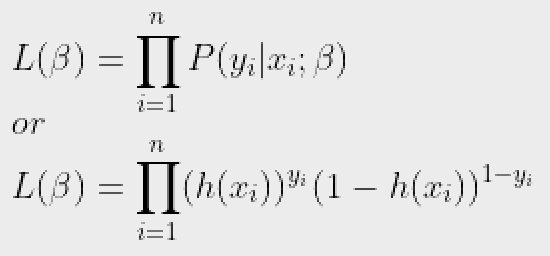
Khả năng xảy ra không là gì ngoài xác suất của dữ liệu (ví dụ đào tạo), được cung cấp cho một mô hình và các giá trị tham số cụ thể (tại đây B,). Nó đo lường sự hỗ trợ được cung cấp bởi dữ liệu cho mỗi giá trị có thể có của B. Chúng ta có được nó bằng cách nhân tất cả P(yi|xi) cho đã cho B.
Và để tính toán dễ dàng hơn, chúng ta có khả năng ghi nhật ký:
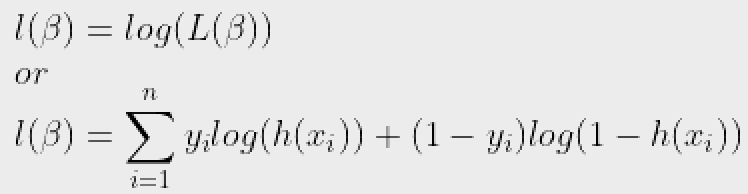
Hàm chi phí cho hồi quy logistic tỷ lệ nghịch với khả năng xảy ra của các tham số. Do đó, chúng ta có thể nhận được một biểu thức cho hàm chi phí, J bằng cách sử dụng phương trình khả năng log như sau:
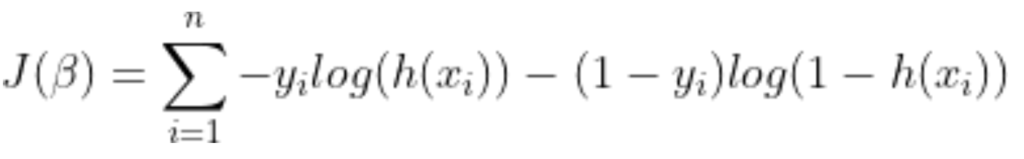
và mục đích của chúng ta là ước tính B sao cho hàm chi phí được giảm thiểu !!
2. Sử dụng thuật toán Gradient descent
Đầu tiên, chúng ta lấy các đạo hàm riêng của mỗi J(b) w.r.t với bj thuộc b để suy ra quy tắc giảm độ dốc ngẫu nhiên (chúng ta chỉ trình bày giá trị dẫn xuất cuối cùng ở đây):
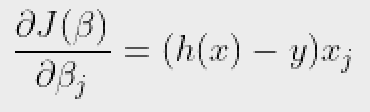
Ở đây, y và h (x) đại diện cho vectơ phản hồi và vectơ phản ứng dự đoán (tương ứng). Ngoài ra, Xj là vectơ đại diện cho các giá trị quan sát của đặc điểm j^th.
Bây giờ, để có được tối thiểu J(b),
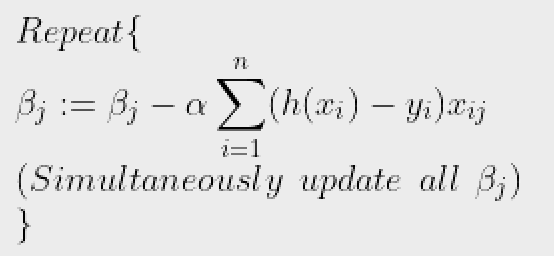
nơi được gọi là tốc độ học tập và cần được đặt rõ ràng.
Hãy để chúng tôi xem cách triển khai python của kỹ thuật trên trên tập dữ liệu mẫu (tải xuống từ đây):
2,25 2,50 2,75 3,00 3,25 3,50 3,75 4,00 4,25 4,50 4,75 5,00 5,50
import csv
import numpy as np
import matplotlib.pyplot as plt
def loadCSV(filename):
'''
function to load dataset
'''
with open(filename,"r") as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return np.array(dataset)
def normalize(X):
'''
function to normalize feature matrix, X
'''
mins = np.min(X, axis = 0)
maxs = np.max(X, axis = 0)
rng = maxs - mins
norm_X = 1 - ((maxs - X)/rng)
return norm_X
def logistic_func(beta, X):
'''
logistic(sigmoid) function
'''
return 1.0/(1 + np.exp(-np.dot(X, beta.T)))
def log_gradient(beta, X, y):
'''
logistic gradient function
'''
first_calc = logistic_func(beta, X) - y.reshape(X.shape[0], -1)
final_calc = np.dot(first_calc.T, X)
return final_calc
def cost_func(beta, X, y):
'''
cost function, J
'''
log_func_v = logistic_func(beta, X)
y = np.squeeze(y)
step1 = y * np.log(log_func_v)
step2 = (1 - y) * np.log(1 - log_func_v)
final = -step1 - step2
return np.mean(final)
def grad_desc(X, y, beta, lr=.01, converge_change=.001):
'''
gradient descent function
'''
cost = cost_func(beta, X, y)
change_cost = 1
num_iter = 1
while(change_cost > converge_change):
old_cost = cost
beta = beta - (lr * log_gradient(beta, X, y))
cost = cost_func(beta, X, y)
change_cost = old_cost - cost
num_iter += 1
return beta, num_iter
def pred_values(beta, X):
'''
function to predict labels
'''
pred_prob = logistic_func(beta, X)
pred_value = np.where(pred_prob >= .5, 1, 0)
return np.squeeze(pred_value)
def plot_reg(X, y, beta):
'''
function to plot decision boundary
'''
# labelled observations
x_0 = X[np.where(y == 0.0)]
x_1 = X[np.where(y == 1.0)]
# plotting points with diff color for diff label
plt.scatter([x_0[:, 1]], [x_0[:, 2]], c='b', label='y = 0')
plt.scatter([x_1[:, 1]], [x_1[:, 2]], c='r', label='y = 1')
# plotting decision boundary
x1 = np.arange(0, 1, 0.1)
x2 = -(beta[0,0] + beta[0,1]*x1)/beta[0,2]
plt.plot(x1, x2, c='k', label='reg line')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.show()
if __name__ == "__main__":
# load the dataset
dataset = loadCSV('dataset1.csv')
# normalizing feature matrix
X = normalize(dataset[:, :-1])
# stacking columns wth all ones in feature matrix
X = np.hstack((np.matrix(np.ones(X.shape[0])).T, X))
# response vector
y = dataset[:, -1]
# initial beta values
beta = np.matrix(np.zeros(X.shape[1]))
# beta values after running gradient descent
beta, num_iter = grad_desc(X, y, beta)
# estimated beta values and number of iterations
print("Estimated regression coefficients:", beta)
print("No. of iterations:", num_iter)
# predicted labels
y_pred = pred_values(beta, X)
# number of correctly predicted labels
print("Correctly predicted labels:", np.sum(y == y_pred))
# plotting regression line
plot_reg(X, y, beta) Estimated regression coefficients: [[ 1.70474504 15.04062212 -20.47216021]]
No. of iterations: 2612
Correctly predicted labels: 100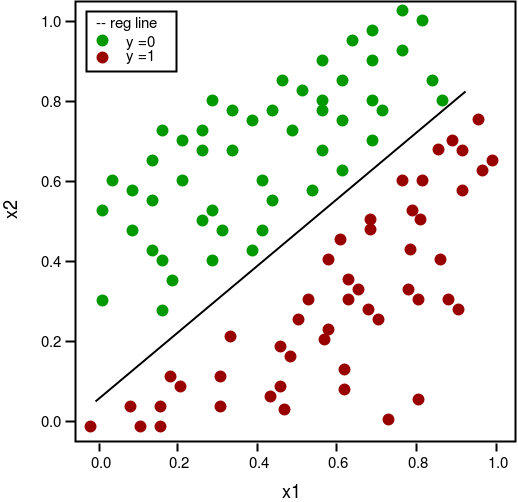
Lưu ý: Gradient descent là một trong nhiều cách để ước tính B.
Về cơ bản, đây là những thuật toán nâng cao hơn có thể dễ dàng chạy bằng Python khi bạn đã xác định hàm chi phí và độ dốc của mình. Các thuật toán này là:
- BFGS (thuật toán Broyden – Fletcher – Goldfarb – Shanno)
- L-BFGS (Giống như BFGS nhưng sử dụng bộ nhớ hạn chế)
- Liên hợp Gradient
3. Ưu điểm / nhược điểm của việc sử dụng bất kỳ một trong các thuật toán này trên Gradient descent:
Ưu điểm
- Không cần chọn tốc độ học
- Thường chạy nhanh hơn (không phải lúc nào cũng vậy)
- Có thể ước tính độ dốc về mặt số học cho bạn (không phải lúc nào cũng hoạt động tốt)
Nhược điểm
- Phức tạp hơn
- Thêm một hộp đen trừ khi bạn tìm hiểu các chi tiết cụ thể
- Hồi quy logistic đa thức
4. Hồi quy logistic đa thức
Trong hồi quy logistic đa thức, biến đầu ra có thể có nhiều hơn hai đầu ra rời rạc. Hãy xem xét Tập dữ liệu số. Ở đây, biến đầu ra là giá trị chữ số có thể nhận các giá trị trong số (0, 12, 3, 4, 5, 6, 7, 8, 9).
Dưới đây là việc triển khai hồi quy Logisitc đa thức bằng cách sử dụng scikit-learning để đưa ra dự đoán trên tập dữ liệu chữ số.
from sklearn import datasets, linear_model, metrics
# load the digit dataset
digits = datasets.load_digits()
# defining feature matrix(X) and response vector(y)
X = digits.data
y = digits.target
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=1)
# create logistic regression object
reg = linear_model.LogisticRegression()
# train the model using the training sets
reg.fit(X_train, y_train)
# making predictions on the testing set
y_pred = reg.predict(X_test)
# comparing actual response values (y_test) with predicted response values (y_pred)
print("Logistic Regression model accuracy(in %):",
metrics.accuracy_score(y_test, y_pred)*100) Logistic Regression model accuracy(in %): 95.6884561892Cuối cùng, đây là một số điểm về hồi quy Logistic cần suy ngẫm:
- KHÔNG giả định mối quan hệ tuyến tính giữa biến phụ thuộc và các biến độc lập, nhưng nó giả định mối quan hệ tuyến tính giữa logit của các biến giải thích và phản hồi.
- Các biến độc lập thậm chí có thể là số hạng lũy thừa hoặc một số phép biến đổi phi tuyến khác của các biến độc lập ban đầu.
- Biến phụ thuộc KHÔNG cần phải được phân phối chuẩn, nhưng nó thường giả định một phân phối từ họ hàm mũ (ví dụ: nhị thức, Poisson, đa thức, bình thường,…); hồi quy logistic nhị phân giả định phân phối nhị thức của phản hồi.
- Tính đồng nhất của phương sai KHÔNG cần phải thỏa mãn.
- Các lỗi cần phải độc lập nhưng KHÔNG được phân phối bình thường.
- Nó sử dụng ước tính khả năng xảy ra tối đa (MLE) chứ không phải bình phương nhỏ nhất thông thường (OLS) để ước tính các tham số và do đó dựa trên các phép gần đúng mẫu lớn.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)
