Hồi quy tuyến tính:
Đây là loại cơ bản và thường được sử dụng để phân tích dự đoán. Đây là một cách tiếp cận thống kê để mô hình hóa mối quan hệ giữa một biến phụ thuộc và một tập hợp các biến độc lập nhất định.
Đây là hai loại:
- Hồi quy tuyến tính cơ bản
- Hồi quy nhiều tuyến tính
Hôm nay cafedev sẽ thảo luận về hồi quy nhiều tuyến tính bằng Python.
Hồi quy nhiều tuyến tính cố gắng mô hình hóa mối quan hệ giữa hai hoặc nhiều đối tượng và phản hồi bằng cách điều chỉnh một phương trình tuyến tính với dữ liệu quan sát được. Các bước để thực hiện hồi quy tuyến tính nhiều lần gần như tương tự như hồi quy tuyến tính đơn giản. Sự khác biệt nằm trong đánh giá. Chúng ta có thể sử dụng nó để tìm ra yếu tố nào có tác động cao nhất đến sản lượng dự đoán và hiện tại các biến số khác nhau có liên quan với nhau.
Ở đây: Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 + …… bn * xn
Y = biến phụ thuộc và x1, x2, x3, …… xn = nhiều biến độc lập
Nội dung chính
1. Giả định về mô hình hồi quy:
- Tuyến tính: Mối quan hệ giữa các biến phụ thuộc và độc lập phải là tuyến tính.
- Độ co giãn đồng nhất: Nên duy trì phương sai không đổi của các sai số.
- Tính chuẩn mực đa biến: Hồi quy đa biến giả định rằng các phần dư được phân phối chuẩn.
- Thiếu đa cộng tuyến: Người ta cho rằng có rất ít hoặc không có đa cộng tuyến trong dữ liệu.
2. Các biến giả
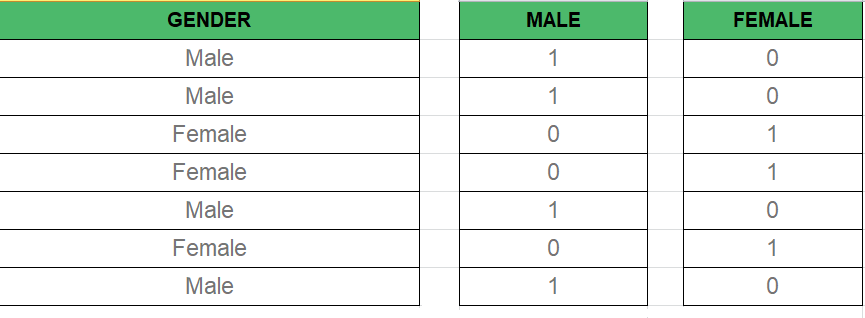
Như chúng ta đã biết trong Mô hình hồi quy nhiều, chúng ta sử dụng rất nhiều dữ liệu phân loại. Sử dụng Dữ liệu phân loại là một phương pháp tốt để đưa dữ liệu không phải số vào Mô hình hồi quy tương ứng. Dữ liệu phân loại đề cập đến các giá trị dữ liệu đại diện cho các giá trị dữ liệu danh mục với số lượng giá trị cố định và không có thứ tự, chẳng hạn như giới tính (nam / nữ). Trong mô hình hồi quy, các giá trị này có thể được biểu diễn bằng Biến giả.
Biến này bao gồm các giá trị như 0 hoặc 1 đại diện cho sự có mặt và không có giá trị phân loại.
3. Các biến bẩy giả
Biến Bẫy giả là một điều kiện trong đó hai hoặc nhiều hơn có tương quan cao. Nói một cách dễ hiểu, chúng ta có thể nói rằng một biến có thể được dự đoán từ dự đoán của biến kia. Giải pháp của biến Bẫy giả là bỏ một biến phân loại. Vì vậy, nếu có m biến Dummy thì m-1 biến được sử dụng trong mô hình.
D2 = D1-1
Đây D2, D1 = Biến giả
Phương pháp xây dựng mô hình:
- Tất cả trong
- Loại bỏ ngược
- Lựa chọn chuyển tiếp
- Loại bỏ hai chiều
- So sánh điểm
Loại bỏ ngược:
Bước # 1: Chọn một mức quan trọng để bắt đầu trong mô hình.
Bước # 2: Điều chỉnh mô hình đầy đủ với tất cả các dự đoán có thể.
Bước # 3: Xem xét công cụ dự đoán có giá trị P cao nhất. Nếu P> SL chuyển đến BƯỚC 4, nếu không thì mô hình đã Sẵn sàng.
Bước # 4: Xóa công cụ dự đoán.
Bước # 5: Điều chỉnh mô hình không có biến này.
Chuyển tiếp-Lựa chọn:
Bước # 1: Chọn mức ý nghĩa để nhập mô hình (ví dụ: SL = 0,05)
Bước # 2: Phù hợp với tất cả các mô hình hồi quy đơn giản y ~ x (n). Chọn cái có giá trị P thấp nhất.
Bước # 3: Giữ biến này và phù hợp với tất cả các mô hình có thể có với một công cụ dự đoán bổ sung được thêm vào (các) công cụ bạn đã có.
Bước # 4: Xem xét công cụ dự đoán có giá trị P thấp nhất. Nếu P <SL, hãy chuyển sang Bước # 3, nếu không thì mô hình đã Sẵn sàng.
Các bước liên quan đến bất kỳ mô hình hồi quy tuyến tính nhiều
Bước # 1: Xử lý trước dữ liệu
- Nhập các thư viện.
- Nhập Tập dữ liệu.
- Mã hóa dữ liệu phân loại.
- Tránh biến Bẫy giả.
- Tách Tập dữ liệu thành Tập huấn luyện và Tập kiểm tra.
Bước # 2: Kết hợp nhiều hồi quy tuyến tính với tập huấn luyện
Bước # 3: Dự đoán kết quả bộ Kiểm tra.
Mã 1:
import numpy as np
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def generate_dataset(n):
x = []
y = []
random_x1 = np.random.rand()
random_x2 = np.random.rand()
for i in range(n):
x1 = i
x2 = i/2 + np.random.rand()*n
x.append([1, x1, x2])
y.append(random_x1 * x1 + random_x2 * x2 + 1)
return np.array(x), np.array(y)
x, y = generate_dataset(200)
mpl.rcParams['legend.fontsize'] = 12
fig = plt.figure()
ax = fig.gca(projection ='3d')
ax.scatter(x[:, 1], x[:, 2], y, label ='y', s = 5)
ax.legend()
ax.view_init(45, 0)
plt.show()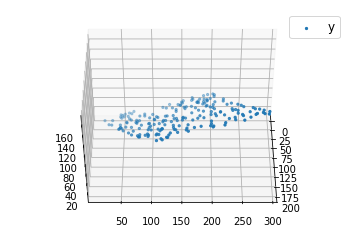 
def mse(coef, x, y):
return np.mean((np.dot(x, coef) - y)**2)/2
def gradients(coef, x, y):
return np.mean(x.transpose()*(np.dot(x, coef) - y), axis = 1)
def multilinear_regression(coef, x, y, lr, b1 = 0.9, b2 = 0.999, epsilon = 1e-8):
prev_error = 0
m_coef = np.zeros(coef.shape)
v_coef = np.zeros(coef.shape)
moment_m_coef = np.zeros(coef.shape)
moment_v_coef = np.zeros(coef.shape)
t = 0
while True:
error = mse(coef, x, y)
if abs(error - prev_error) <= epsilon:
break
prev_error = error
grad = gradients(coef, x, y)
t += 1
m_coef = b1 * m_coef + (1-b1)*grad
v_coef = b2 * v_coef + (1-b2)*grad**2
moment_m_coef = m_coef / (1-b1**t)
moment_v_coef = v_coef / (1-b2**t)
delta = ((lr / moment_v_coef**0.5 + 1e-8) *
(b1 * moment_m_coef + (1-b1)*grad/(1-b1**t)))
coef = np.subtract(coef, delta)
return coef
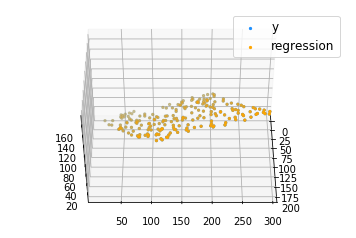
coef = np.array([0, 0, 0])
c = multilinear_regression(coef, x, y, 1e-1)
fig = plt.figure()
ax = fig.gca(projection ='3d')
ax.scatter(x[:, 1], x[:, 2], y, label ='y',
s = 5, color ="dodgerblue")
ax.scatter(x[:, 1], x[:, 2], c[0] + c[1]*x[:, 1] + c[2]*x[:, 2],
label ='regression', s = 5, color ="orange")
ax.view_init(45, 0)
ax.legend()
plt.show() Output
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
