Dữ liệu đơn biến là kiểu dữ liệu trong đó kết quả chỉ phụ thuộc vào một biến. Ví dụ, tập dữ liệu của các điểm trên một đường có thể được coi là dữ liệu đơn biến trong đó abscissa có thể được coi là đặc điểm đầu vào và tọa độ có thể được coi là đầu ra / kết quả.
Ví dụ:
Cho dòng Y = 2X + 3;
Đặc điểm đầu vào là X và Y sẽ là kết quả.
| X | Y |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
Ý tưởng:
Đối với hồi quy tuyến tính đơn biến, chỉ có một vectơ đặc trưng đầu vào. Đường hồi quy sẽ có dạng:
Y = b0 + b1 * X
Ở đây,
b0 và b1 là các hệ số của hồi quy.
Do đó, nó đang được cố gắng dự đoán các hệ số hồi quy b0 và b1 bằng cách đào tạo một mô hình.
1. Các chức năng tiện ích
1.1 .Dự đoán
def predict(x, b0, b1):
"""Predicts the value of prediction based on
current value of regression coefficients when input is x"""
# Y = b0 + b1 * X
return b0 + b1 * x 1.2 Chức năng ước lượng :
Hàm Cost tính toán tỷ lệ phần trăm lỗi với giá trị hiện tại của hệ số hồi quy. Nó xác định một cách định lượng các hệ số hồi quy wrt thực của mô hình có tỷ lệ sai sót thấp nhất.
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
def cost(x, y, b0, b1):
# y is a list of expected value
errors = []
for x, y in zip(x, y):
prediction = predict(x, b0, b1)
expected = y
difference = prediction-expected
errors.append(difference)
# Now, we have errors for all the observations,
# for some input, the value of error might be positive
# and for some input might be negative,
# and if we directly add them up,
# the values might cancel out leading to wrong output."
# Hence, we use concept of mean squared error.
# in mse, we return mean of square of all the errors.
mse = sum([e * e for e in errors])/len(errors)
return mse 1.3.Chi phí phái sinh
Sau mỗi lần lặp, chi phí được nâng cấp tương ứng với lỗi. Bản chất của lỗi là dữ liệu rất nhạy cảm. Theo dữ liệu nhạy cảm, có nghĩa là giá trị lỗi thay đổi rất nhanh, bởi vì chúng ta đã bình phương trong hàm lỗi. Do đó, để làm cho nó dễ chịu hơn với các giá trị lỗi cao, chúng ta lấy ra hàm lỗi.
Toán học như sau:

Code:
def cost_derivative(x, y, b0, b1, i):
return sum([
2*(predict(xi, b0, b1)-yi)*1
if i == 0
else 2*(predict(xi, b0, b1)-yi)*xi
for xi, yi in zip(x, y)
])/len(x) 1.4.Cập nhật Hệ số:
Tại mỗi lần lặp (kỷ nguyên), các giá trị của hệ số hồi quy được cập nhật bởi một giá trị cụ thể wrt đối với lỗi từ lần lặp trước. Bản cập nhật này rất quan trọng và là mấu chốt của các ứng dụng ML mà bạn viết.
Cập nhật các hệ số một cách chính xác Việc cập nhật một hệ số được thực hiện bằng cách phạt giá trị của nó bằng một phần lỗi mà các giá trị trước đó đã gây ra.
Phần này được gọi là tỷ lệ học tập. Điều này xác định tốc độ mô hình của chúng ta đạt đến điểm hội tụ (điểm mà lỗi lý tưởng là 0).
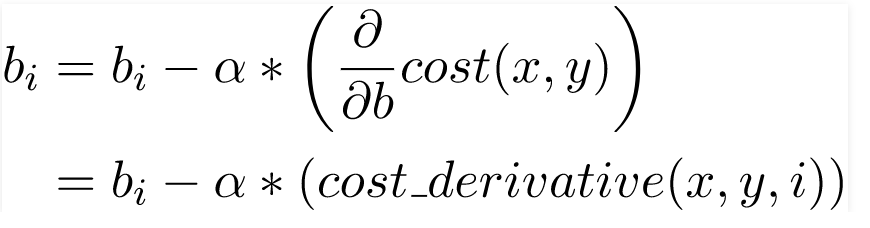
Hàm Python như sau:
def update_coeff(x, y, b0, b1, i, alpha):
bi -= alpha * cost_derivative(x, y, b0, b1, i)
return bi 1.5.Ngừng lặp lại:
Đây là hàm được sử dụng để chỉ định khi nào nên dừng các bước lặp.
Theo người dùng, thuật toán stop_iteration thường trả về true trong các điều kiện sau:
- Lặp lại tối đa: Mô hình được đào tạo cho một số lần lặp cụ thể.
- Giá trị lỗi: Tùy thuộc vào giá trị của lỗi trước đó, thuật toán quyết định tiếp tục hay dừng.
- Độ chính xác: Tùy thuộc vào độ chính xác cuối cùng của mô hình, nếu nó lớn hơn độ chính xác đã đề cập, thuật toán trả về True,
- Kết hợp: Điều này thường được sử dụng hơn. Điều này kết hợp nhiều hơn một điều kiện đã đề cập ở trên cùng với một tùy chọn nghỉ ngơi đặc biệt. Nghỉ ngơi đặc biệt là điều kiện mà việc đào tạo tiếp tục cho đến khi điều gì đó tồi tệ xảy ra. Điều gì đó không tốt có thể bao gồm tràn kết quả, vượt quá giới hạn thời gian, v.v.
Có tất cả các chức năng tiện ích được xác định, hãy xem giả mã được thực hiện theo sau:
x, y is the given data.
(b0, b1) <-- (0, 0)
i = 0
while True:
if stop_iteration(i):
break
else:
b0 = update_coeff(x, y, b0, b1, 0, alpha)
b1 = update_coeff(x, y, b0, b1, 1, alpha) Triển khai Oop cuối cùng:
# -----------------------------------------------------------
#Cafedev.vn - Kênh thông tin IT hàng đầu Việt Nam
#@author cafedevn
#Contact: cafedevn@gmail.com
#Fanpage: https://www.facebook.com/cafedevn
#Group: https://www.facebook.com/groups/cafedev.vn/
#Instagram: https://instagram.com/cafedevn
#Twitter: https://twitter.com/CafedeVn
#Linkedin: https://www.linkedin.com/in/cafe-dev-407054199/
#Pinterest: https://www.pinterest.com/cafedevvn/
#YouTube: https://www.youtube.com/channel/UCE7zpY_SlHGEgo67pHxqIoA/
# -----------------------------------------------------------
class LinearRegressor:
def __init__(self, x, y, alpha = 0.01, b0 = 0, b1 = 0):
"""
x: input feature
y: result / target
alpha: learning rate, default is 0.01
b0, b1: linear regression coefficient.
"""
self.i = 0
self.x = x
self.y = y
self.alpha = alpha
self.b0 = b0
self.b1 = b1
if len(x) != len(y):
raise TypeError("x and y should have same number of rows.")
def predict(model, x):
"""Predicts the value of prediction based on
current value of regression coefficients when input is x"""
# Y = b0 + b1 * X
return model.b0 + model.b1 * x
def cost_derivative(model, i):
x, y, b0, b1 = model.x, model.y, model.b0, model.b1
predict = model.predict
return sum([
2 * (predict(xi) - yi) * 1
if i == 0
else (predict(xi) - yi) * xi
for xi, yi in zip(x, y)
]) / len(x)
def update_coeff(model, i):
cost_derivative = model.cost_derivative
if i == 0:
model.b0 -= model.alpha * cost_derivative(i)
elif i == 1:
model.b1 -= model.alpha * cost_derivative(i)
def stop_iteration(model, max_epochs = 1000):
model.i += 1
if model.i == max_epochs:
return True
else:
return False
def fit(model):
update_coeff = model.update_coeff
model.i = 0
while True:
if model.stop_iteration():
break
else:
update_coeff(0)
update_coeff(1)
if __name__ == '__main__':
linearRegressor = LinearRegressor(
x =[i for i in range(12)],
y =[2 * i + 3 for i in range(12)],
alpha = 0.03
)
linearRegressor.fit()
print(linearRegressor.predict(12))
# expects 2 * 12 + 3 = 27 Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!