Phương trình chuẩn là một cách tiếp cận phân tích đối với hồi quy tuyến tính với chi phí hàm bình phương thấp nhất. Chúng ta có thể trực tiếp tìm ra giá trị của θ mà không cần sử dụng Gradient Descent. Làm theo cách tiếp cận này là một lựa chọn hiệu quả và tiết kiệm thời gian khi đang làm việc với một tập dữ liệu có các tính năng nhỏ.
Nội dung chính
1. Phương trình chuẩn như sau:
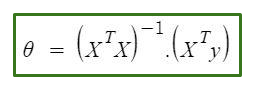
Trong phương trình trên,
θ: tham số giả thuyết xác định nó tốt nhất.
X: Giá trị thuộc tính đầu vào của mỗi phiên bản.
Y: Giá trị đầu ra của mỗi phiên bản.
2. Toán học đằng sau phương trình
Cho hàm giả thuyết
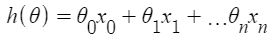
n: cái không của các thuộc tính trong tập dữ liệu.
x0: 1 (cho phép nhân vectơ)
Lưu ý rằng đây là tích chấm giữa các giá trị θ và x. Vì vậy, để thuận tiện cho việc giải quyết, chúng ta có thể viết nó là:
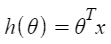
Động cơ trong Hồi quy tuyến tính là giảm thiểu chi phí hàm:
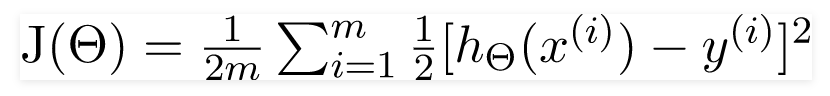
xi: giá trị đầu vào của ví dụ huấn luyện iih.
m: không. các trường hợp đào tạo
n: không. của các thuộc tính tập dữ liệu
yi: kết quả mong đợi của phiên bản thứ i
Hãy để chúng ta biểu diễn chi phí hàm dưới dạng vectơ.
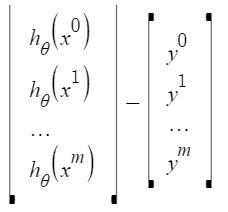
chúng ta đã bỏ qua 1 / 2m ở đây vì nó sẽ không tạo ra bất kỳ sự khác biệt nào trong công việc. Nó được sử dụng để thuận tiện trong toán học trong khi tính toán gradient giảm dần. Nhưng nó không cần thiết ở đây nữa.
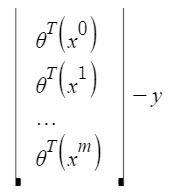
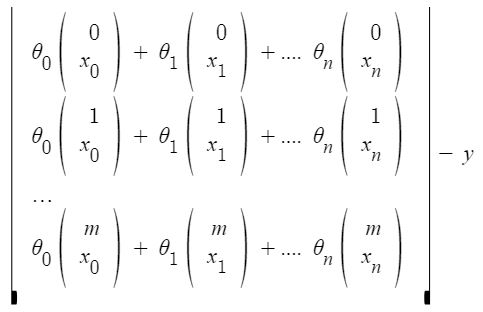
xij: giá trị của thuộc tính jih trong ví dụ huấn luyện iih.
Điều này có thể được giảm xuống
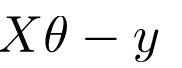
Nhưng mỗi giá trị còn lại là bình phương. Chúng ta không thể đơn giản bình phương biểu thức trên Vì bình phương của một vectơ / ma trận không bằng bình phương của mỗi giá trị của nó. Vì vậy, để nhận được giá trị bình phương, hãy nhân vectơ / ma trận với chuyển vị của nó. Vì vậy, phương trình cuối cùng được suy ra là
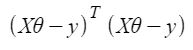
Do đó, chi phí hàm là
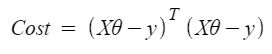
Vì vậy, bây giờ nhận giá trị của θ bằng cách sử dụng đạo hàm
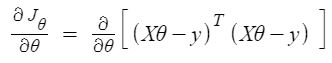
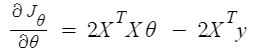
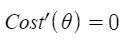
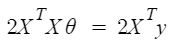
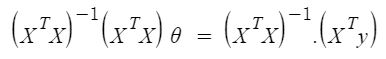
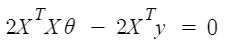
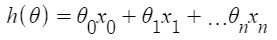
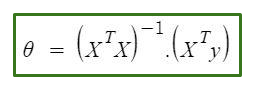
Vì vậy, đây là phương trình chuẩn cuối cùng được suy ra với θ cho giá trị chi phí tối thiểu.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)
