Bài viết này thảo luận về những điều cơ bản của hồi quy tuyến tính và cách triển khai nó trong ngôn ngữ lập trình Python.
Hồi quy tuyến tính là một cách tiếp cận thống kê để mô hình hóa mối quan hệ giữa một biến phụ thuộc với một tập hợp các biến độc lập nhất định.
Lưu ý: Trong bài viết này, chúng ta đề cập đến các biến phụ thuộc là phản hồi và các biến độc lập là các đặc tính để đơn giản hóa.
Để cung cấp hiểu biết cơ bản về hồi quy tuyến tính, chúng ta bắt đầu với phiên bản cơ bản nhất của hồi quy tuyến tính, tức là hồi quy tuyến tính đơn giản(Simple Linear Regression).
Nội dung chính
1. Hồi quy tuyến tính cơ bản(Simple Linear Regression)
Hồi quy tuyến tính đơn giản là một cách tiếp cận để dự đoán phản hồi bằng cách sử dụng một đặc tính duy nhất.
Giả thiết rằng hai biến có liên quan tuyến tính. Do đó, chúng ta cố gắng tìm một hàm tuyến tính dự đoán giá trị phản hồi (y) chính xác nhất có thể như một hàm của tính năng hoặc biến độc lập (x).
Hãy để chúng ta xem xét một tập dữ liệu trong đó chúng ta có giá trị của phản hồi y cho mọi đặc tính x:
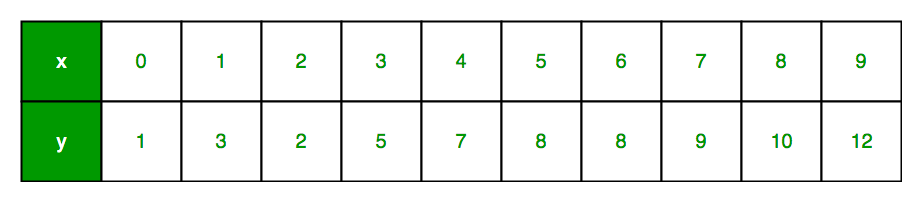
Thông thường, chúng ta xác định:
x dưới dạng vectơ đặc trưng, tức là x = [x_1, x_2,…., x_n],
y là vectơ phản hồi, tức là y = [y_1, y_2,…., y_n]
cho n quan sát (trong ví dụ trên, n = 10).
Biểu đồ phân tán của tập dữ liệu trên trông giống như:
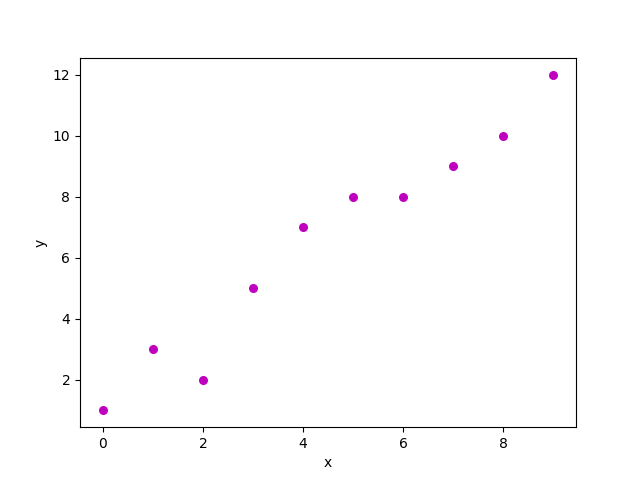
Bây giờ, nhiệm vụ là tìm một đường phù hợp nhất với biểu đồ phân tán ở trên để chúng ta có thể dự đoán phản hồi cho bất kỳ giá trị đặt tính mới nào. (tức là giá trị của x không có trong tập dữ liệu)
Đường này được gọi là đường hồi quy.
Phương trình của đường hồi quy được biểu diễn như sau:
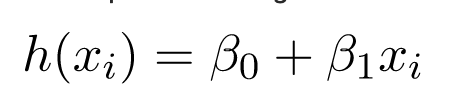
Trong đó:
- h (x_i) đại diện cho giá trị phản hồi dự đoán cho lần quan sát thứ i.
- b_0 và b_1 lần lượt là các hệ số hồi quy và đại diện cho hệ số chặn y và độ dốc của đường hồi quy.
Để tạo mô hình của chúng ta, chúng ta phải “học” hoặc ước tính giá trị của các hệ số hồi quy b_0 và b_1. Và sau khi đã ước tính các hệ số này, chúng ta có thể sử dụng mô hình để dự đoán phản hồi!
Trong bài viết này, chúng ta sẽ sử dụng kỹ thuật Least Squares.
Bây giờ hãy xem xét:
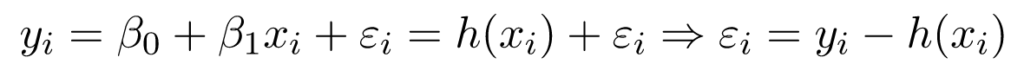
Ở đây, e_i là lỗi còn lại trong lần quan sát thứ i.
Vì vậy, mục đích của chúng ta là giảm thiểu tổng sai số dư.
Chúng ta xác định lỗi bình phương hoặc chi phí hàm, J là:
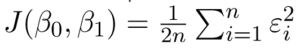
và nhiệm vụ của chúng ta là tìm giá trị của b_0 và b_1 mà J (b_0, b_1) là nhỏ nhất!
Không đi sâu vào chi tiết toán học, chúng ta trình bày kết quả ở đây:
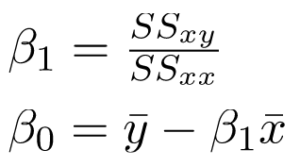
trong đó SS_xy là tổng các độ lệch chéo của y và x:
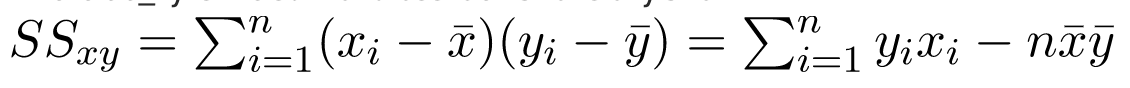
và SS_xx là tổng các độ lệch bình phương của x:
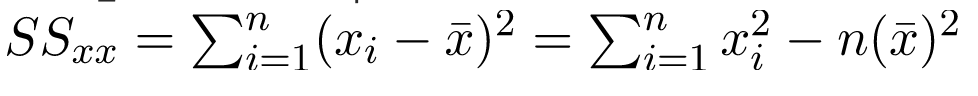
Lưu ý: Có thể tìm thấy công thức hoàn chỉnh để tìm ước lượng bình phương nhỏ nhất trong hồi quy tuyến tính đơn giản.
Tải tại đây
Dưới đây là cách triển khai code python với kỹ thuật trên trên tập dữ liệu nhỏ của chúng ta:
import numpy as np
import matplotlib.pyplot as plt
def estimate_coef(x, y):
# number of observations/points
n = np.size(x)
# mean of x and y vector
m_x, m_y = np.mean(x), np.mean(y)
# calculating cross-deviation and deviation about x
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x
# calculating regression coefficients
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)
def plot_regression_line(x, y, b):
# plotting the actual points as scatter plot
plt.scatter(x, y, color = "m",
marker = "o", s = 30)
# predicted response vector
y_pred = b[0] + b[1]*x
# plotting the regression line
plt.plot(x, y_pred, color = "g")
# putting labels
plt.xlabel('x')
plt.ylabel('y')
# function to show plot
plt.show()
def main():
# observations
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12])
# estimating coefficients
b = estimate_coef(x, y)
print("Estimated coefficients:\nb_0 = {} \
\nb_1 = {}".format(b[0], b[1]))
# plotting regression line
plot_regression_line(x, y, b)
if __name__ == "__main__":
main() Đầu ra của đoạn code trên là:
Estimated coefficients:
b_0 = -0.0586206896552
b_1 = 1.45747126437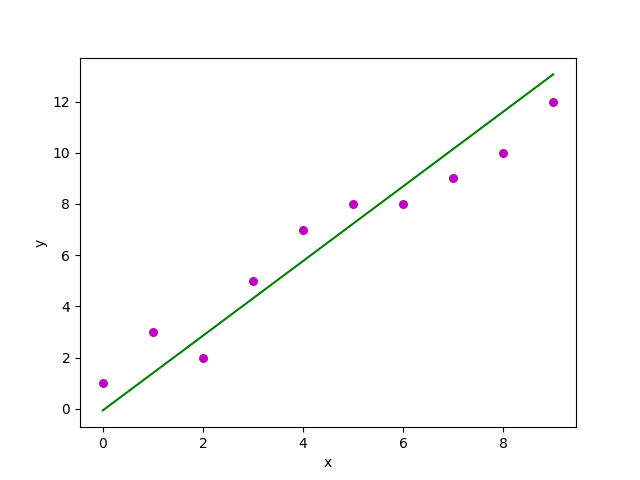
2. Hồi quy nhiều tuyến tính
Nhiều hồi quy tuyến tính cố gắng mô hình hóa mối quan hệ giữa hai hoặc nhiều đặc điểm và phản hồi bằng cách điều chỉnh phương trình tuyến tính với dữ liệu quan sát được.
Rõ ràng, nó không là gì khác ngoài một phần mở rộng của hồi quy tuyến tính đơn giản.
Hãy xem xét một tập dữ liệu với p đặt điểm(hoặc biến độc lập) và một phản hồi (hoặc biến phụ thuộc).
Ngoài ra, tập dữ liệu chứa n hàng / quan sát.
Chúng ta xác định:
X (ma trận đặc trưng) = ma trận cỡ n X p trong đó x_ {ij} biểu thị các giá trị của đặc điểm thứ j cho lần quan sát thứ i.
Vì thế,
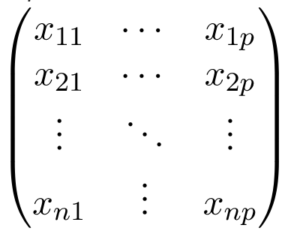
và
y (vectơ phản hồi) = vectơ có kích thước n trong đó y_ {i} biểu thị giá trị của phản ứng cho lần quan sát thứ i.
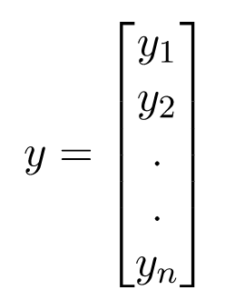
Đường hồi quy cho p đối tượng được biểu diễn như sau:
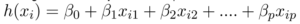
trong đó h (x_i) là giá trị phản hồi dự đoán cho lần quan sát thứ i và b_0, b_1,…, b_p là các hệ số hồi quy.
Ngoài ra, chúng ta có thể viết:
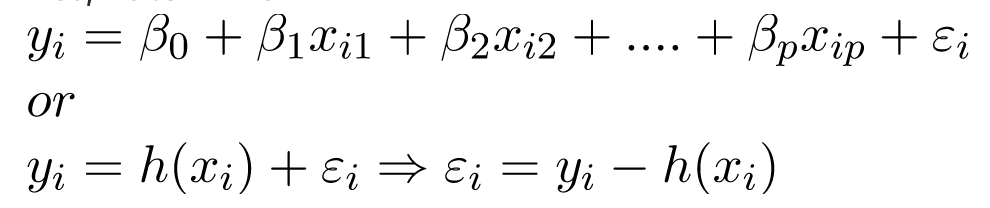
trong đó e_i đại diện cho sai số còn lại trong lần quan sát thứ i.
Chúng ta có thể tổng quát hóa mô hình tuyến tính của mình hơn một chút bằng cách biểu diễn ma trận đặc trưng X dưới dạng:

Vì vậy, bây giờ, mô hình tuyến tính có thể được biểu diễn dưới dạng ma trận như sau:
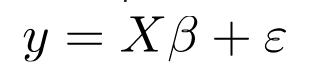
Ở đâu,
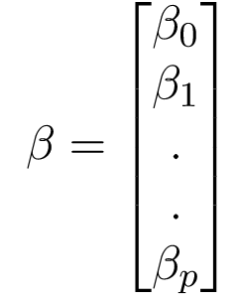
và

Bây giờ, chúng ta xác định ước tính của b, tức là b ’bằng phương pháp Bình phương nhỏ nhất.
Như đã được giải thích, phương pháp Least Squares có xu hướng xác định b ’mà tổng sai số dư được giảm thiểu.
Chúng ta trình bày kết quả trực tiếp tại đây:
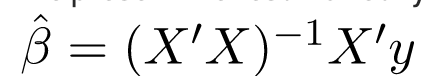
trong đó ‘biểu diễn chuyển vị của ma trận trong khi -1 biểu thị nghịch đảo của ma trận.
Khi biết các ước lượng bình phương nhỏ nhất, b ’, mô hình hồi quy tuyến tính bội số hiện có thể được ước tính là:
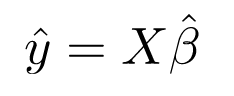
trong đó y ’là vectơ phản hồi ước tính.
Lưu ý: Bạn có thể tìm thấy phương pháp hoàn chỉnh để có được ước lượng bình phương nhỏ nhất trong hồi quy tuyến tính bội số bên dưới.
Tải tại đây
Dưới đây là việc triển khai kỹ thuật hồi quy nhiều tuyến tính trên tập dữ liệu định giá nhà ở Boston bằng cách sử dụng Scikit-learning.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics
# load the boston dataset
boston = datasets.load_boston(return_X_y=False)
# defining feature matrix(X) and response vector(y)
X = boston.data
y = boston.target
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=1)
# create linear regression object
reg = linear_model.LinearRegression()
# train the model using the training sets
reg.fit(X_train, y_train)
# regression coefficients
print('Coefficients: \n', reg.coef_)
# variance score: 1 means perfect prediction
print('Variance score: {}'.format(reg.score(X_test, y_test)))
# plot for residual error
## setting plot style
plt.style.use('fivethirtyeight')
## plotting residual errors in training data
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
## plotting residual errors in test data
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
## plotting line for zero residual error
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
## plotting legend
plt.legend(loc = 'upper right')
## plot title
plt.title("Residual errors")
## function to show plot
plt.show() Đầu ra của chương trình trên có dạng như sau:
Coefficients:
[ -8.80740828e-02 6.72507352e-02 5.10280463e-02 2.18879172e+00
-1.72283734e+01 3.62985243e+00 2.13933641e-03 -1.36531300e+00
2.88788067e-01 -1.22618657e-02 -8.36014969e-01 9.53058061e-03
-5.05036163e-01]
Variance score: 0.720898784611và biểu đồ Lỗi còn lại trông như thế này:
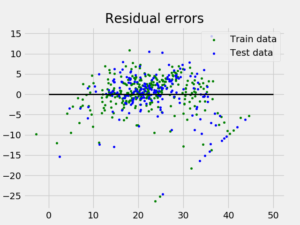
Trong ví dụ trên, chúng ta xác định điểm chính xác bằng cách sử dụng Điểm phương sai được giải thích.
Chúng ta xác định:
Giải thích_variance_score = 1 – Var {y – y ’} / Var {y}
trong đó y ’là đầu ra mục tiêu ước tính, y là đầu ra mục tiêu tương ứng (đúng) và Var là Phương sai, bình phương của độ lệch chuẩn.
Điểm tốt nhất có thể là 1,0, các giá trị thấp hơn sẽ tệ hơn.
3. Giả định
Dưới đây là các giả định cơ bản mà mô hình hồi quy tuyến tính đưa ra liên quan đến tập dữ liệu mà nó được áp dụng:
- Mối quan hệ tuyến tính: Mối quan hệ giữa các biến phản hồi và đặt điểm phải là mối quan hệ tuyến tính. Giả định về độ tuyến tính có thể được kiểm tra bằng cách sử dụng biểu đồ phân tán. Như hình dưới đây, hình 1 đại diện cho các biến có liên quan tuyến tính trong đó các biến trong hình 2 và 3 rất có thể là phi tuyến tính. Vì vậy, hình 1 sẽ đưa ra các dự đoán tốt hơn bằng cách sử dụng hồi quy tuyến tính.
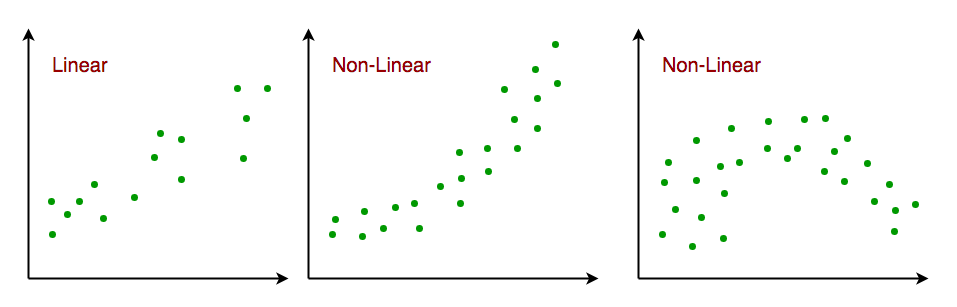
- Ít hoặc không có nhiều tuyến: Người ta cho rằng có rất ít hoặc không có đa cộng tuyến trong dữ liệu. Đa cộng tuyến xảy ra khi các đặc trưng (hoặc các biến độc lập) không độc lập với nhau.
- Ít hoặc không có tự tương quan: Một giả định khác là có rất ít hoặc không có tự tương quan trong dữ liệu. Tự tương quan xảy ra khi các sai số dư không độc lập với nhau. Bạn có thể tham khảo tại đây để có cái nhìn sâu sắc hơn về chủ đề này.
- Độ co giãn đồng nhất (Homoscedasticity): Độ co giãn đồng nhất mô tả tình huống trong đó thuật ngữ sai số (nghĩa là “nhiễu” hoặc xáo trộn ngẫu nhiên trong mối quan hệ giữa các biến độc lập và biến phụ thuộc) là giống nhau trên tất cả các giá trị của các biến độc lập. Như hình bên dưới, hình 1 có phương thay đổi trong khi hình 2 có phương sai thay đổi.
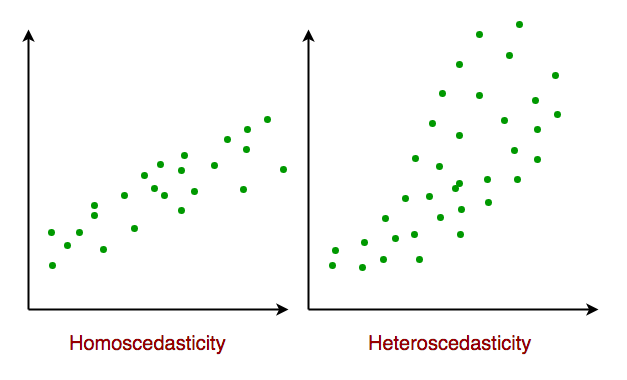
Khi chúng ta đi đến phần cuối của bài viết này, chúng ta sẽ thảo luận về một số ứng dụng của hồi quy tuyến tính dưới đây.
4. Các ứng dụng:
1. Đường xu hướng: Đường xu hướng biểu thị sự thay đổi của một số dữ liệu định lượng theo thời gian (như GDP, giá dầu, v.v.). Các xu hướng này thường tuân theo một mối quan hệ tuyến tính. Do đó, hồi quy tuyến tính có thể được áp dụng để dự đoán các giá trị trong tương lai. Tuy nhiên, phương pháp này thiếu giá trị khoa học trong trường hợp các thay đổi tiềm ẩn khác có thể ảnh hưởng đến dữ liệu.
2. Kinh tế học: Hồi quy tuyến tính là công cụ thực nghiệm chủ yếu trong kinh tế học. Ví dụ: nó được sử dụng để dự đoán chi tiêu tiêu dùng, chi tiêu đầu tư cố định, đầu tư hàng tồn kho, mua hàng xuất khẩu của một quốc gia, chi tiêu cho nhập khẩu, nhu cầu nắm giữ tài sản lưu động, nhu cầu lao động và cung lao động.
3. Tài chính: Mô hình tài sản giá vốn sử dụng hồi quy tuyến tính để phân tích và định lượng rủi ro hệ thống của một khoản đầu tư.
4. Sinh học: Hồi quy tuyến tính được sử dụng để mô hình hóa mối quan hệ nhân quả giữa các thông số trong hệ thống sinh học.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!








![[Tự học C++] Số dấu phẩy động(float, double,…) trong C++](https://cafedev.vn/wp-content/uploads/2019/12/cafedevn_c_develoment-100x70.jpg)
