Sử dụng Hồi quy tuyến tính, tất cả các dự đoán> = 0,5 có thể được coi là 1 và phần còn lại <0,5 có thể được coi là 0. Nhưng sau đó câu hỏi đặt ra tại sao không thể thực hiện phân loại bằng cách sử dụng nó?
Nội dung chính
1. Vấn đề
Giả sử chúng ta đang phân loại một thư là thư rác hay không phải thư rác và đầu ra của chúng ta là y, nó có thể là 0 (thư rác) hoặc 1 (không phải thư rác). Trong trường hợp Hồi quy tuyến tính, hθ (x) có thể> 1 hoặc <0. Mặc dù dự đoán của chúng ta phải nằm trong khoảng từ 0 đến 1, mô hình sẽ dự đoán giá trị nằm ngoài phạm vi, tức là có thể> 1 hoặc <0.
Vì vậy, đó là lý do tại sao đối với nhiệm vụ Phân loại, Hồi quy Logistic / Sigmoid đóng vai trò của nó.
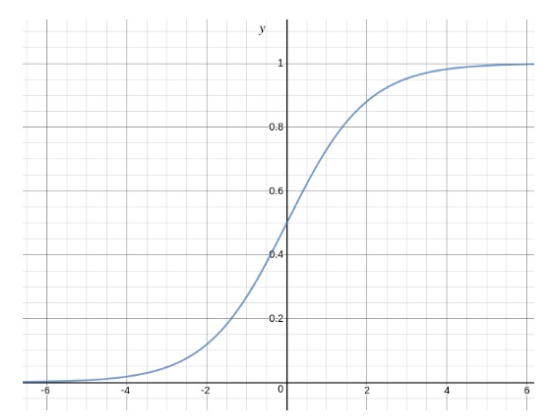
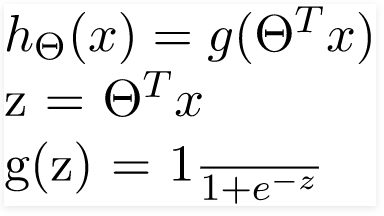
Ở đây, chúng ta cắm θTx vào hàm logistic trong đó θ là trọng số / tham số và x là đầu vào và hθ (x) là hàm giả thiết. g () là hàm sigmoid.
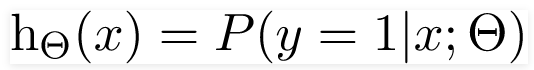
Có nghĩa là xác suất y = 1 khi x được tham số hóa thành θ
Để nhận các giá trị rời rạc 0 hoặc 1 để phân loại, các ranh giới rời rạc được xác định. Giả thuyết hàm cab được dịch là
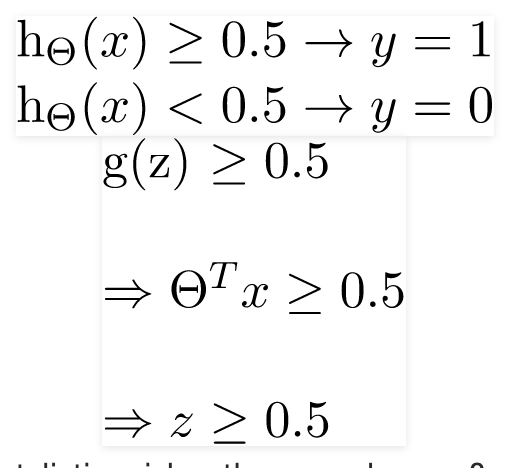
Ranh giới Quyết định là đường phân biệt khu vực nơi y = 0 và nơi y = 1. Các ranh giới quyết định này là kết quả của hàm giả thuyết đang được xem xét.
2. Tìm hiểu Ranh giới Quyết định với một ví dụ –
Giả sử hàm của chúng ta là
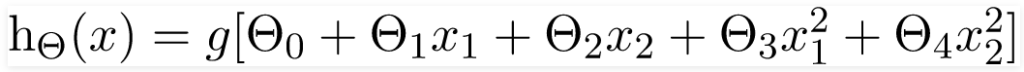
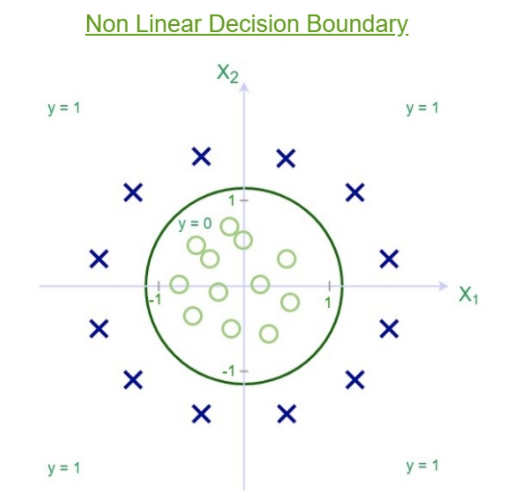
Sau đó, ranh giới quyết định trông giống như
Cho biết trọng lượng hoặc thông số là
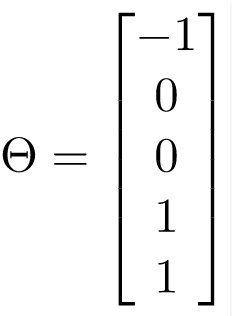
Vì vậy, nó dự đoán y = 1 nếu
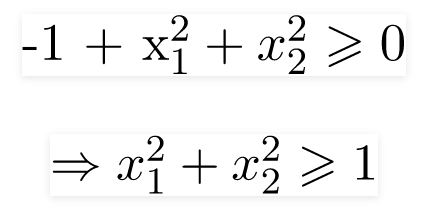
Và đó là phương trình của một đường tròn có bán kính = 1 và gốc là tâm. Đây là ranh giới quyết định cho giả thuyết đã xác định của chúng tôi.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
