Hồi quy đa thức là một dạng hồi quy tuyến tính trong đó mối quan hệ giữa biến độc lập x và biến phụ thuộc y được mô hình hóa dưới dạng đa thức bậc n. Hồi quy đa thức phù hợp với mối quan hệ phi tuyến giữa giá trị của x và giá trị trung bình có điều kiện tương ứng của y, được ký hiệu là E (y | x)
Nội dung chính
1. Tại sao dùng hồi quy đa thức:
- Có một số mối quan hệ mà một nhà nghiên cứu sẽ giả thuyết là đường cong. Rõ ràng, loại trường hợp như vậy sẽ bao gồm một số hạng đa thức.
- Kiểm tra lượng dư. Nếu chúng ta cố gắng điều chỉnh một mô hình tuyến tính cho phù hợp với dữ liệu cong, thì một biểu đồ phân tán của phần dư (trục Y) trên bộ dự đoán (trục X) sẽ có các bản vá của nhiều phần dư dương ở giữa. Do đó trong tình huống như vậy là không thích hợp.
- Một giả định trong phân tích hồi quy tuyến tính bội thông thường là tất cả các biến độc lập là độc lập. Trong mô hình hồi quy đa thức, giả thiết này không được thỏa mãn.
2. Công dụng của hồi quy đa thức:
Chúng về cơ bản được sử dụng để xác định hoặc mô tả hiện tượng phi tuyến tính như:
- Tốc độ phát triển của các mô.
- Tiến triển của dịch bệnh
- Phân bố đồng vị cacbon trong trầm tích hồ
Mục tiêu cơ bản của phân tích hồi quy là mô hình hóa giá trị kỳ vọng của một biến phụ thuộc y theo giá trị của một biến độc lập x. Trong hồi quy đơn giản, chúng ta sử dụng phương trình sau:
y = a + bx + e
Ở đây y là biến phụ thuộc, a là hệ số chặn của y, b là hệ số góc và e là tỷ lệ lỗi.
Trong nhiều trường hợp, mô hình tuyến tính này sẽ không hoạt động. Ví dụ, nếu chúng ta phân tích quá trình sản xuất tổng hợp hóa học theo nhiệt độ mà quá trình tổng hợp diễn ra trong những trường hợp như vậy, chúng ta sử dụng mô hình bậc hai
y = a + b1x + b2 ^ 2 + e
Ở đây y là biến phụ thuộc vào x, a là chặn y và e là tỷ lệ lỗi.
Nói chung, chúng ta có thể mô hình hóa nó cho giá trị thứ n.
y = a + b1x + b2x ^ 2 + …. + bnx ^ n
Vì hàm hồi quy là tuyến tính theo các biến chưa biết, do đó các mô hình này là tuyến tính từ điểm ước lượng.
Do đó, thông qua kỹ thuật Least Square, hãy tính giá trị phản hồi là y.
3. Hồi quy đa thức trong Python:
Để có được Tập dữ liệu được sử dụng để phân tích hồi quy đa thức, hãy nhấp vào đây.
Bước 1: Nhập thư viện và tập dữ liệu
Nhập các thư viện quan trọng và tập dữ liệu chúng ta đang sử dụng để thực hiện hồi quy đa thức
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
datas = pd.read_csv('data.csv')
datas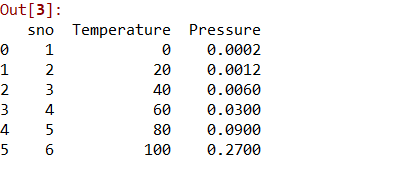 
Bước 2: Chia tập dữ liệu thành 2 thành phần
Chia tập dữ liệu thành hai thành phần là X và y. X sẽ chứa Cột từ 1 đến 2. y sẽ chứa cột 2.
X = datas.iloc[:, 1:2].values
y = datas.iloc[:, 2].values Bước 3: Kết hợp hồi quy tuyến tính với tập dữ liệu
Phù hợp với mô hình hồi quy tuyến tính Trên hai thành phần.
# Fitting Linear Regression to the dataset
from sklearn.linear_model import LinearRegression
lin = LinearRegression()
lin.fit(X, y) Bước 4: Gắn hồi quy đa thức vào tập dữ liệu
Phù hợp với mô hình hồi quy đa thức trên hai thành phần X và y.
# Fitting Polynomial Regression to the dataset
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 4)
X_poly = poly.fit_transform(X)
poly.fit(X_poly, y)
lin2 = LinearRegression()
lin2.fit(X_poly, y)
Bước 5: Trong bước này, chúng ta đang Hình dung kết quả Hồi quy tuyến tính bằng cách sử dụng biểu đồ phân tán.
# Visualising the Linear Regression results
plt.scatter(X, y, color = 'blue')
plt.plot(X, lin.predict(X), color = 'red')
plt.title('Linear Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()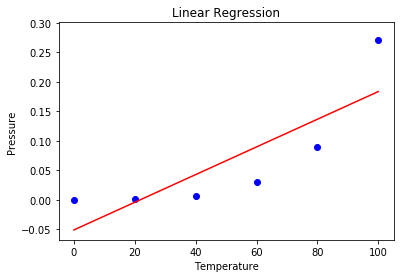 
Bước 6: Hình dung kết quả hồi quy đa thức bằng cách sử dụng biểu đồ phân tán.
# Visualising the Polynomial Regression results
plt.scatter(X, y, color = 'blue')
plt.plot(X, lin2.predict(poly.fit_transform(X)), color = 'red')
plt.title('Polynomial Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()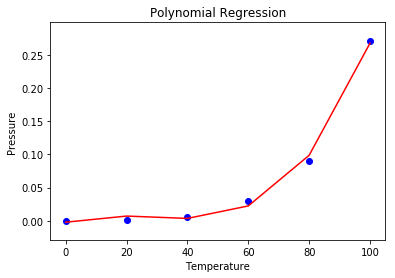 
Bước 7: Dự đoán kết quả mới với cả hồi quy tuyến tính và đa thức.
# Predicting a new result with Linear Regression
lin.predict(110.0)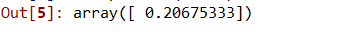
# Predicting a new result with Polynomial Regression
lin2.predict(poly.fit_transform(110.0))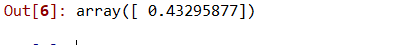 
Ưu điểm của việc sử dụng hồi quy đa thức:
- Phạm vi rộng của hàm có thể được phù hợp với nó.
- Đa thức về cơ bản phù hợp với nhiều độ cong.
- Đa thức cung cấp giá trị gần đúng nhất của mối quan hệ giữa biến phụ thuộc và biến độc lập.
Nhược điểm của việc sử dụng hồi quy đa thức
- Chúng quá nhạy cảm với các yếu tố ngoại lai.
- Sự hiện diện của một hoặc hai điểm ngoại lệ trong dữ liệu có thể ảnh hưởng nghiêm trọng đến kết quả của một phân tích phi tuyến.
- Ngoài ra, đáng tiếc là có ít công cụ xác thực mô hình hơn để phát hiện các giá trị ngoại lệ trong hồi quy phi tuyến so với hồi quy tuyến tính.
Cài ứng dụng cafedev để dễ dàng cập nhật tin và học lập trình mọi lúc mọi nơi tại đây.
Nguồn và Tài liệu tiếng anh tham khảo:
Tài liệu từ cafedev:
- Full series tự học Python từ cơ bản tới nâng cao tại đây nha.
- Tự học ML bằng Python từ cơ bản tới nâng cao.
- Ebook về python tại đây.
- Các series tự học lập trình MIỄN PHÍ khác
- Nơi liên hệ hợp tác hoặc quảng cáo cùng Cafedevn tại đây.
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
Chào thân ái và quyết thắng!
